Problem A. 892. (November 2024)

A. 892. Given two integers, \(\displaystyle k\) and \(\displaystyle d\) such that \(\displaystyle d\) divides \(\displaystyle k^3-2\). Show that there exists integers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) satisfying \(\displaystyle d=a^3+2b^3+4c^3-6abc\).

Proposed by Csongor Beke and László Bence Simon, Cambridge

(7 pont)

Deadline expired on December 10, 2024.

Let \(\displaystyle k\) be an integer satisfying \(\displaystyle k^3\equiv 2\pmod{d}\). Now let's use the well known identity \(\displaystyle x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)\):

Thus \(\displaystyle d\mid a^3+2b^3+2c^3-6abc\) is following from \(\displaystyle d|a+kb+k^2c\). Let \(\displaystyle S\subset \mathbb{Z}^3\) be defined by property \(\displaystyle d|a+kb+k^2c\).

We will first show that \(\displaystyle S\) is a three dimensional lattice, i.e. it's possible to find three non-zero vectors \(\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3\) such that \(\displaystyle S=\left\{\kappa \mathbf{u}_1+\lambda\mathbf{v}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu \in \mathbb{Z}\right\}\) and the volume of the paralelepipedon defined by \(\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3\) is \(\displaystyle d\).

Let vectors \(\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3 \in S\setminus \{\mathbf{0}\}\) be defined as linearly independent and minimizing the volume of the paralelepipedon (such vectors exist since the volume of the paralelelpipedon defined by three linearly independent integer vectors is a positive integer). Clearly if \(\displaystyle \mathbf{u}, \mathbf{v}\in S\), then \(\displaystyle \mathbf{u}\pm\mathbf{v}\in S\), therefore

\(\displaystyle \left\{\kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu\in \mathbb{Z}\right\}\subset S.\)

Suppose vector \(\displaystyle \mathbf{v}\in S\) is not contained in the set above. Let's consider the translated version of the paralelepipedon defined by \(\displaystyle \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3\) by vector \(\displaystyle \kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3\) that contains \(\displaystyle v\). Now if we swap \(\displaystyle \mathbf{u_3}\) with \(\displaystyle v-\kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3\), we get a paralelepipedon with a smaller volume, which is a contradiction. Therefore

\(\displaystyle \left\{\kappa\mathbf{u}_1+\lambda\mathbf{u}_2+\mu\mathbf{u}_3:\kappa, \lambda, \mu\in \mathbb{Z}\right\}= S.\)

We have to show that the volume of the paralelepipedon is \(\displaystyle d\). First observe that \(\displaystyle [0,d-1]^3\cap S\) has exactly \(\displaystyle d^2\) elements: indeed, after choosing the values of \(\displaystyle b\) and \(\displaystyle c\) there is a single choice for the value of \(\displaystyle a\) such that the divisibility condition holds. Let \(\displaystyle D\) denote the diameter and \(\displaystyle T\) the volume of our paralelepipedon. Now considering cube \(\displaystyle Q_n=[0,dn-1]^3\), we can show with a similar argument that exactly \(\displaystyle d^2n^3\) elements of \(\displaystyle S\) are in \(\displaystyle Q_n\). However, trying to cover this cube with our paralelepipedons, we see that at least \(\displaystyle (nd-2d)^3/T\) is completely contained in \(\displaystyle Q_n\), and it can also be covered with \(\displaystyle (nd+2D)^3/T\) copies of it, This means that \(\displaystyle (nd-2D)^3\le k^2\cdot n^3\cdot T\le (nd+2D)^3\), which implies \(\displaystyle T=d\).

No we want to show that there exists \(\displaystyle (a,b,c)\neq (0,0,0)\) satisfying

\(\displaystyle f(a,b,c)=|a^3+2b^3+4c^3-6abc|<3d. \)

This would complete our proof: if \(\displaystyle f(a,b,c)=-d\), then \(\displaystyle f(-a,-b,-c)=d\). If \(\displaystyle f(a,b,c)=2d\), then \(\displaystyle a\) must be even, and then \(\displaystyle f(b,c,a/2)=d\). If \(\displaystyle f(a,b,c)=-2d\), then \(\displaystyle f(-b,-c,-a/2)=d\). Finally \(\displaystyle f(a,b,c)=0\) is not possible, since in this case \(\displaystyle a\) is even, and so \(\displaystyle f(b,c,a/2)=0\). This could be continued indefinitely, which is impossible for integer triples different from \(\displaystyle (0,0,0)\).

To prove our claim we will use Minkowski's theorem stating that if there is a convex set symmetric to the origin with a volume of at least \(\displaystyle 8d\), it has to contain a lattice point different from the origin. So if we can find a convex shape that is symmetric to the origin with a volume of at least \(\displaystyle 8d\) the points of which satisfying \(\displaystyle f(a,b,c)<3d\), we are done. To make our formulas symmetric let's apply an affinity to the plane \(\displaystyle x=0\) of ratio \(\displaystyle 2^{-\frac{1}{3}}\), and then an affinity of ratio \(\displaystyle 2^{\frac{1}{3}}\) to plane \(\displaystyle z=0\). Since the product of the ratios is 1, this transformation preserves volume, and

\(\displaystyle f(x,y,z)=2(x')^3+2y^3+2(z')^3-2(3x'yz')=2g(x',y,z'). \)

Thus we are looking for a convex shape symmetric to the origin with a volume of at least \(\displaystyle 8d\) inside region \(\displaystyle g(x,y,z)<1.5d\).

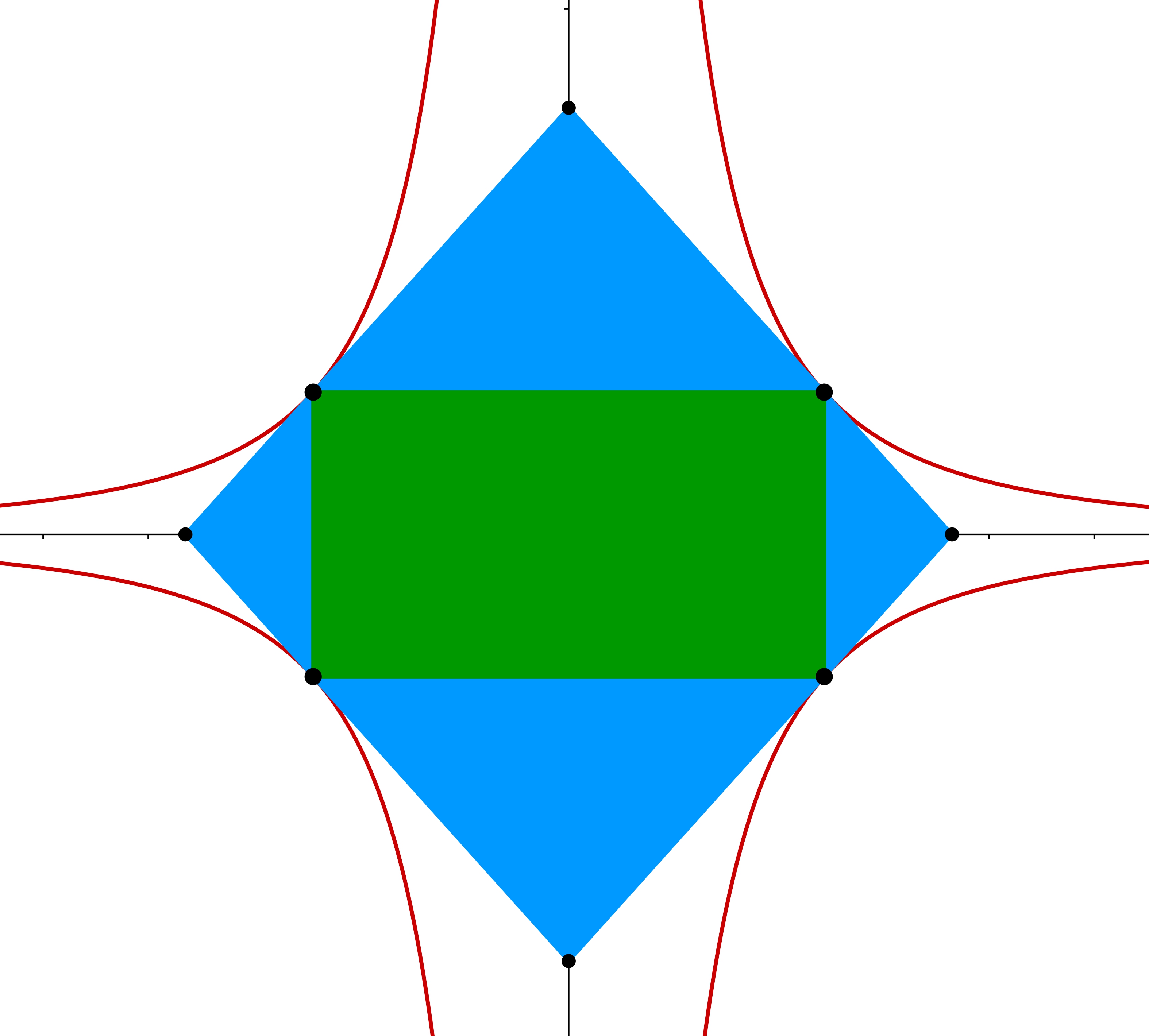
Amazingly, function \(\displaystyle g(x,y,z)\) has a geometric meaning. Scalar product \(\displaystyle \frac{(1,1,1)}{\sqrt{3}}\cdot (x,y,z)=\frac{x+y+z}{\sqrt{3}}\) is the component of vector \(\displaystyle (x,y,z)\) parallel to \(\displaystyle (1,1,1)\), thus by the Pythagorean theorem the square of the distance of point \(\displaystyle (x,y,z)\) from line \(\displaystyle (t,t,t)\) is

\(\displaystyle f_2(x,y,z)^2=x^2+y^2+z^2-\left(\frac{x+y+z}{3}\right)^2=\frac{2}{3}(x^2+y^2+z^2-xy-yz-zx). \)

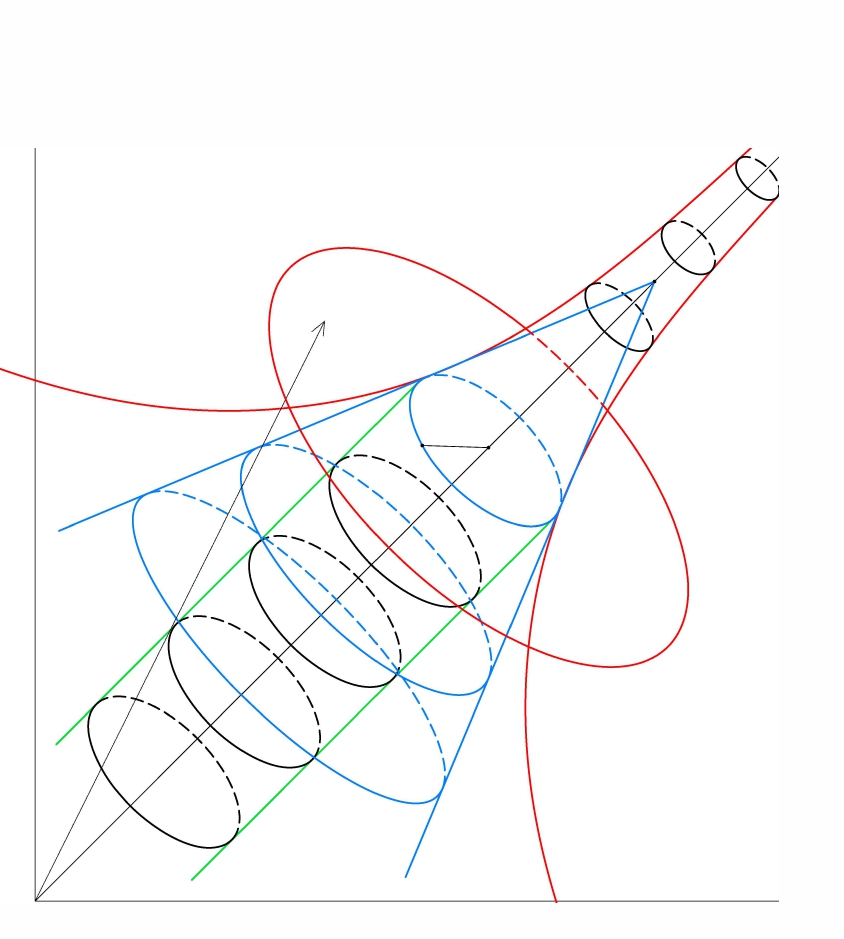
What will be the geometric meaning when we multiply this with \(\displaystyle f_1(x,y,z)=\frac{x+y+z}{\sqrt{3}}\)? This is the volume of the following shape: take point \(\displaystyle (x,y,z)\), rotate it around line \(\displaystyle (t,t,t)\), and reflect the resulting circle across the origin. The two circles define a cylinder with volume

\(\displaystyle 2\cdot f_1(x,y,z)\cdot f_2(x,y,z)^2=2\cdot \frac{x+y+z}{\sqrt{3}}\cdot \frac{2}{3}(x^2+y^2+z^2-xy-yz-zx)\cdot \pi=g(x,y,z)\cdot \frac{4\pi}{\sqrt{3}}. \)

This gives us the idea to pick a point \(\displaystyle P\) on surface \(\displaystyle g(x,y,z)=1.5d\), say \(\displaystyle P=\frac{\sqrt[3]{3d}}{2}(1,1,2)\), and consider the cylinder above. The volume we get this way is \(\displaystyle g(P)\cdot \frac{4\pi}{3\sqrt{3}}=\frac{2\pi d}{\sqrt{3}}\), which is not large enough unfortunately. However, if we consider a double cone containing this cylinder tangent to surface \(\displaystyle g(x,y,z)=1.5d\), we will get a volume greater than \(\displaystyle 8d\). Let's see the details. First define \(\displaystyle K_P\) as points satisfying

\(\displaystyle \left|\frac{1}{3}\cdot \frac{f_1(x,y,z)}{f_1(P)}\right|+\left|\frac{2}{3}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|<1. \)

The points of \(\displaystyle K_P\) satisfy (by using the AM-GM inequality)

\(\displaystyle \left|\frac{g(x,y,z)}{g(P)}\right|=\left|\frac{f_1(x,y,z)}{f_1(P)}\cdot \frac{f_2(x,y,z)}{f_2(P)}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|\leq \left(\left|\frac{1}{3}\cdot \frac{f_1(x,y,z)}{f_1(P)}\right|+\left|\frac{2}{3}\cdot \frac{f_2(x,y,z)}{f_2(P)}\right|\right)^3<1. \)

so \(\displaystyle K_P\) is contained in \(\displaystyle g(x,y,z)<1.5d\) (since \(\displaystyle g(x,y,z)<g(P)=1.5d\)). The geometric meaning of \(\displaystyle K_P\) is a double cone which is convex and symmetric to the origin. Now let's find its volume: the height of the cone is \(\displaystyle 3f_1(P)\), and the radius of its base circle is \(\displaystyle \frac{3}{2}f_2(P)\), so its volume is \(\displaystyle \frac{1}{3} \cdot \left(\frac{3}{2}\right)^2 \cdot 3=\frac{9}{4}\) times as big as the volume of our previous cylinder, i.e. it's \(\displaystyle \frac{4.5\pi d}{\sqrt{3}}\), and this is more than \(\displaystyle 8d\) since \(\displaystyle \pi^3>\frac{256}{27}\).

Cross section:

Draft of our surface, cylinder and cone:

Statistics:

11 students sent a solution.
7 points:	Bodor Mátyás, Diaconescu Tashi, Holló Martin, Varga Boldizsár.
6 points:	Forrai Boldizsár, Minh Hoang Tran, Szakács Ábel.
1 point:	1 student.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, November 2024