 Problem B. 3873. (January 2006)
Problem B. 3873. (January 2006)
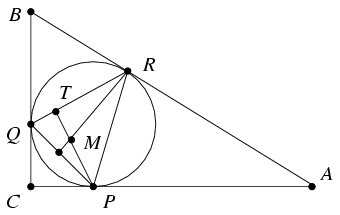
B. 3873. The inscribed circle of the right-angled triangle ABC touches the leg AC at P, the leg BC at Q and the hypotenuse AB at R. Let M denote the orthocentre of the triangle PQR. Prove that RM=PQ.
Suggested by L. Gerőcs, Budapest
(3 pont)
Deadline expired on February 15, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Mivel APR és BQR egyenlőszárú háromszögek, könnyen kiszámolhatjuk, hogy a PRQ szög 45o-os. Ha a PQR háromszögben a PM magasság talppontja T, akkor a TPR háromszög egyenlőszárú derékszögű háromszög lesz, vagyis PT=RT. Mivel pedig a TPQ szög egyenlő a TRM szöggel, a TPQ és TRM derékszögű háromszögek egybevágók, tehát PQ=RM.
Statistics:
135 students sent a solution. 3 points: 122 students. 2 points: 7 students. 1 point: 6 students.
Problems in Mathematics of KöMaL, January 2006
