 Problem B. 3877. (January 2006)
Problem B. 3877. (January 2006)
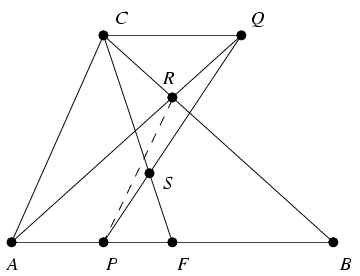
B. 3877. The centroid of the triangle ABC is S, and the midpoint of AB is F. For an interior point P of the line segment AF, consider that point Q of the line PS for which QC and AB are parallel. Let R be the intersection of the lines QA and BC. Prove that the line segment PR halves the area of the triangle ABC.
(4 pont)
Deadline expired on February 15, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Az ABR és QCR háromszögek hasonlóságából
Mindkét oldalhoz 1-et hozzádva
adódik. Mivel pedig CS=2FS, a QCS és PFS háromszögek hasonlósága alapján QC=2PF, vagyis QC+AB=2PF+2BF=2BP. Ezért
Mindkét oldalt az ABC szög szinuszának felével beszorozva a feladatban szereplő állítást kapjuk.
Statistics:
91 students sent a solution. 4 points: 77 students. 3 points: 7 students. 2 points: 4 students. 1 point: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, January 2006
