 Problem B. 4248. (February 2010)
Problem B. 4248. (February 2010)
B. 4248. Denote the centres of the escribed circles of a triangle ABC by Oa, Ob, Oc, the centre of the incircle by I, and the radius of the circumscribed circle by R. Let A1 be the intersection of the perpendiculars dropped from point Ob onto line AB and from point Oc onto line AC. Show that A1I=2R.
(5 pont)
Deadline expired on March 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A háromszög szögeit jelölje a szokásos módon \(\displaystyle \alpha,\beta,\gamma\). Az \(\displaystyle O_b\) pontnak az \(\displaystyle AC\) oldalra, illetve az \(\displaystyle AB\) oldalegyenesre való merőleges vetületét jelölje \(\displaystyle E\) és \(\displaystyle F\). Mivel az \(\displaystyle AO_b\) egyenes felezi a \(\displaystyle 180^\circ-\alpha\) nagyságú \(\displaystyle EAF\) szöget, az \(\displaystyle AEO_b\) és \(\displaystyle AFO_b\) derékszögű háromszögekben \(\displaystyle EAO_b\sphericalangle=FAO_b\sphericalangle=90^\circ-\alpha/2\) és \(\displaystyle EO_bA\sphericalangle=FO_bA\sphericalangle=A_1O_bO_c\sphericalangle=\alpha/2\). Ugyanígy az \(\displaystyle A_1O_cO_b\) szög nagysága is \(\displaystyle \alpha/2\), vagyis \(\displaystyle A_1O_bO_c\) olyan egyenlőszárú háromszög, melynek \(\displaystyle A_1\)-nél lévő csúcsszöge \(\displaystyle O_bA_1O_c\sphericalangle=180^\circ-\alpha\).
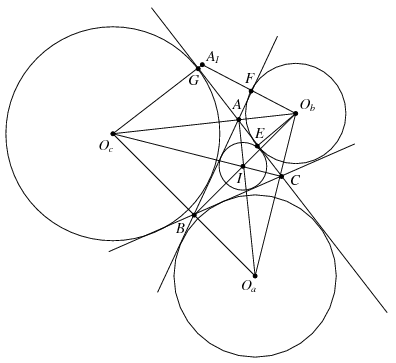
Mivel \(\displaystyle CAI\sphericalangle=CAO_a\sphericalangle=\alpha/2\), látható, hogy az \(\displaystyle O_bAO_a\), és ugyanilyen alapon az \(\displaystyle O_cAO_a\) szög is derékszög, vagyis az \(\displaystyle AIO_a\) egyenes merőleges az \(\displaystyle O_bAO_c\) egyenesre. Ezek szerint az \(\displaystyle O_aO_bO_c\) háromszögnek az eredeti \(\displaystyle ABC\) háromszög a talpponti háromszöge, vagyis az \(\displaystyle ABC\) háromszög köré írt kör az \(\displaystyle O_aO_bO_c\) háromszög Feuerbach-köre. Ezért az \(\displaystyle O_aO_bO_c\) háromszög köré írható kör sugara \(\displaystyle 2R\). Ennek a \(\displaystyle K\) körnek a középpontját jelölje \(\displaystyle O'\).
Az \(\displaystyle EO_bA\) szöghöz hasonlóan kiszámolható, hogy \(\displaystyle EO_bC\sphericalangle=\gamma/2\), vagyis \(\displaystyle O_cO_bO_a\sphericalangle=AO_bC\sphericalangle=(\alpha+\gamma)/2\), és ugyanígy \(\displaystyle O_bO_cO_a\sphericalangle=(\alpha+\beta)/2\), \(\displaystyle O_bO_aO_c\sphericalangle=(\beta+\gamma)/2=90^\circ-\alpha/2\). Ezért a \(\displaystyle K\) körben az \(\displaystyle O_bO_c\) húrhoz tartozó középponti szög \(\displaystyle O_bO'O_c\sphericalangle=180^\circ-\alpha\). Látható tehát, hogy az \(\displaystyle A_1O_bO_c\) és az \(\displaystyle O'O_bO_c\) egyenlőszárú háromszögek egybevágók, vagyis \(\displaystyle A_1O_b=A_1O_c=O'O_b=O'O_c=2R\). Mivel
\(\displaystyle O_bIO_c\sphericalangle=180^\circ-O_cO_bI\sphericalangle- O_bO_cI\sphericalangle=180^\circ-\frac{\gamma}{2}-\frac{\beta}{2}= 90^\circ+\frac{\alpha}{2}\)
és \(\displaystyle O_bA_1O_c\sphericalangle=180^\circ-\alpha=360^\circ-2\cdot O_bIO_c\sphericalangle\), világos, hogy az \(\displaystyle I\) pont az \(\displaystyle A_1\) középpontú, \(\displaystyle O_b\)-n és \(\displaystyle O_c\)-n áthaladó körvonalra illeszkedik. Ezért valóban \(\displaystyle A_1I=A_1O_b=2R\).
Statistics:
22 students sent a solution. 5 points: Damásdi Gábor, Dolgos Tamás, Éles András, Jernei Tamás, Keresztfalvi Tibor, Kiss 902 Melinda Flóra, Korondi Zénó, Márkus Bence, Máthé László, Medek Ákos, Mester Márton, Mészáros András, Milánkovich Dorottya, Nagy Róbert, Popper Dávid, Somogyi Ákos, Strenner Péter, Szabó 928 Attila, Uray Marcell János, Weisz Ágoston. 4 points: Bálint Csaba. 3 points: 1 student.
Problems in Mathematics of KöMaL, February 2010
