 Problem B. 4369. (May 2011)
Problem B. 4369. (May 2011)
B. 4369. Each of the circles k1, k2 and k3 passes through a point P, and the circles ki and kj also pass through the point Mi,j. Let A be an arbitrary point of circle k1. Let k4 be an arbitrary circle passing through A and M1,2, and let k5 be an arbitrary circle passing through A and M1,3. Show that if the other intersections of the pairs of circles k4 and k2, k5 and k3, k4 and k5 are B, C and D, respectively, then the points M2,3, B, C, D are either concyclic or collinear.
(4 pont)
Deadline expired on June 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Hallgatólagosan feltételezzük, hogy a szóban forgó körök és pontok különbözők (ha pl. az \(\displaystyle A\) pont egybeesne az \(\displaystyle M_{1,2}\) ponttal, akkor a \(\displaystyle k_4\) körnek érintenie kellene a \(\displaystyle k_1\) kört).
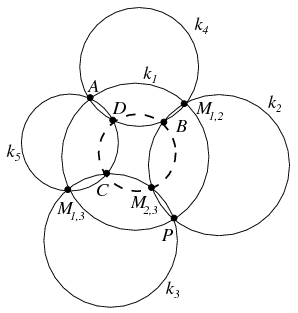
A jelölések alkalmas megváltoztatásával a feladatot a következő áttekinthetőbb formában is megfogalmazhatjuk:
Legyen \(\displaystyle l_1, l_2,l_3,l_4\) négy kör a síkon úgy hogy az \(\displaystyle l_5=l_1\) jelöléssel élve minden \(\displaystyle 1\le i\le 4\) esetén az \(\displaystyle l_i\) és \(\displaystyle l_{i+1}\) körök egymást az \(\displaystyle X_i,Y_i\) pontokban metszik. Ha az \(\displaystyle X_i\) pontok egy körön helyezkednek el, akkor az \(\displaystyle Y_i\) pontok is egy körön vagy egy egyenesen vannak.
A bizonyításhoz a novemberi B. 4308. feladat megoldásához hasonlóan érdemes lesz irányított szögekkel dolgozni, és felhasználni azt a tényt, hogy az egymástól különböző \(\displaystyle P,Q,R,S\) pontok akkor és csak akkor illeszkednek egy körre vagy egy egyenesre, ha modulo \(\displaystyle 180^\circ\) számolva \(\displaystyle PRQ\sphericalangle+QSP\sphericalangle=0\). Ennek megfelelően a továbbiakban az egyenlőséget mindig modulo \(\displaystyle 180^\circ\) értjük majd.
Mivel az \(\displaystyle Y_3Y_2Y_1, Y_1Y_2X_2\) és \(\displaystyle X_2Y_2Y_3\) szögek egymást teljes szöggé egészítik ki,
\(\displaystyle Y_3Y_2Y_1\sphericalangle=-Y_1Y_2X_2\sphericalangle-X_2Y_2Y_3\sphericalangle.\)
Felhasználva, hogy az \(\displaystyle X_1,X_2,Y_1,Y_2\) pontok az \(\displaystyle l_2\) körre, az \(\displaystyle X_2,X_3,Y_2,Y_3\) pontok pedig az \(\displaystyle l_3\) körre illeszkednek, kapjuk, hogy
\(\displaystyle Y_3Y_2Y_1\sphericalangle=-Y_1Y_2X_2\sphericalangle-X_2Y_2Y_3\sphericalangle=X_2X_1Y_1\sphericalangle+Y_3X_3X_2\sphericalangle.\)
A ciklikus szimmetria alapján hasonlóképpen
\(\displaystyle Y_1Y_4Y_3\sphericalangle=X_4X_3Y_3\sphericalangle+Y_1X_1X_4\sphericalangle.\)
A két egyenlőséget összeadva, a tagok átcsoportosítása után
\(\displaystyle Y_3Y_2Y_1\sphericalangle+Y_1Y_4Y_3\sphericalangle=(X_2X_1Y_1\sphericalangle+Y_1X_1X_4\sphericalangle)+ (X_4X_3Y_3\sphericalangle+Y_3X_3X_2\sphericalangle)=\)
\(\displaystyle =X_2X_1X_4\sphericalangle+X_4X_3X_2\sphericalangle=0,\)
hiszen feltettük, hogy az \(\displaystyle X_i\) pontok egy körre esnek. Ez pedig azt jelenti, hogy az \(\displaystyle Y_i\) pontok valóban egy körre vagy egy egyenesre esnek.
Statistics:
12 students sent a solution. 4 points: Ágoston Péter, Bogár Blanka, Lajos Mátyás, Lenger Dániel, Máthé László, Medek Ákos, Simig Dániel, Weisz Gellért. 3 points: Damásdi Gábor, Dolgos Tamás, Hajnal Máté, Nagy Róbert.
Problems in Mathematics of KöMaL, May 2011
