Problem B. 4396. (November 2011)

B. 4396. The inscribed circle of triangle ABC touches side b at F and side a at G. Prove that the foot of the perpendicular dropped from A onto the angle bisector of angle $\beta$ lies on the line FG. (By conventional notation , side b lies opposite to vertex B and angle $\beta$ is the angle at B, etc.)

(3 pont)

Deadline expired on December 12, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A szóban forgó pontot jelölje $\displaystyle P$, a beírt kör középpontját $\displaystyle K$. Mindkét pont a $\displaystyle B$-ből induló $\displaystyle f$ szögfelezőn helyezkedik el. Mivel $\displaystyle AKB\sphericalangle=180^\circ-\alpha/2-\beta/2=90^\circ+\gamma/2>90^\circ$, az $\displaystyle f$ félegyenesen a $\displaystyle K$ pont elválasztja a $\displaystyle P$ pontot a $\displaystyle B$-től. Az $\displaystyle FGC$ egyenlő szárú háromszögben $\displaystyle CGF\sphericalangle=CFG\sphericalangle=90^\circ-\gamma/2$, ezért a $\displaystyle GPB$ háromszögben

$\displaystyle GPB\sphericalangle=180^\circ-FGB\sphericalangle-GBP\sphericalangle= 180^\circ-(90^\circ+\gamma/2)-\beta/2=\alpha/2.$

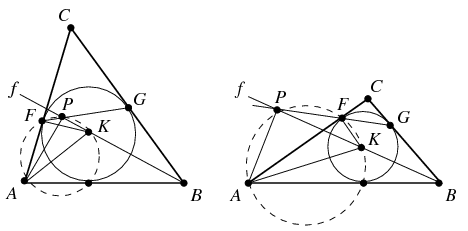
Vegyük észre, hogy $\displaystyle AFK\sphericalangle=APK\sphericalangle=90^\circ$, vagyis az $\displaystyle A,F,K$ és $\displaystyle P$ pontok egy körön helyezkednek el. Ha $\displaystyle P=F$, akkor az állítás nyilvánvaló. Ha $\displaystyle P$ a háromszög belsejébe esik, akkor az $\displaystyle AFPK$ húrnégyszögben $\displaystyle FPK\sphericalangle=180^\circ-FAK\sphericalangle=180^\circ-\alpha/2$. Ezért az $\displaystyle FPB$ és $\displaystyle GPB$ szögek egymást $\displaystyle 180^\circ$-ra egészítik ki, tehát a $\displaystyle P$ pont az $\displaystyle FG$ szakasz belső pontja lesz. Végül ha $\displaystyle P$ a háromszögön kívül helyezkedik el, akkor az $\displaystyle APFK$ húrnégyszögben $\displaystyle FPK\sphericalangle=FAK\sphericalangle=\alpha/2$. Ezért ekkor az $\displaystyle FPB$ és $\displaystyle GPB$ szögek egyenlők, tehát a $\displaystyle P$ pont a $\displaystyle GF$ szakasz $\displaystyle F$-en túli meghosszabbítására esik.

Statistics:

60 students sent a solution.

3 points: Czipó Bence, Di Giovanni Márk, Havasi 0 Márton, Janzer Barnabás, Janzer Olivér, Jenei Adrienn, Kacz Dániel, Katona Dániel, Leitereg Miklós, Maga Balázs, Makk László, Mester Márton, Nagy-György Pál, Papp Roland, Pohl Péter Mátyás, Schwarcz Tamás, Somogyvári Kristóf, Szabó 789 Barnabás, Tekeli Tamás, Tossenberger Tamás, Tulassay Zsolt, Veres Andrea, Weimann Richárd, Weisz Ambrus, Wiandt Péter, Wiandt Zsófia, Zsiros Ádám.

2 points: 28 students.

1 point: 4 students.

0 point: 1 student.

Problems in Mathematics of KöMaL, November 2011

60 students sent a solution.
3 points:	Czipó Bence, Di Giovanni Márk, Havasi 0 Márton, Janzer Barnabás, Janzer Olivér, Jenei Adrienn, Kacz Dániel, Katona Dániel, Leitereg Miklós, Maga Balázs, Makk László, Mester Márton, Nagy-György Pál, Papp Roland, Pohl Péter Mátyás, Schwarcz Tamás, Somogyvári Kristóf, Szabó 789 Barnabás, Tekeli Tamás, Tossenberger Tamás, Tulassay Zsolt, Veres Andrea, Weimann Richárd, Weisz Ambrus, Wiandt Péter, Wiandt Zsófia, Zsiros Ádám.
2 points:	28 students.
1 point:	4 students.
0 point:	1 student.

Already signed up?
New to KöMaL?