Problem B. 4413. (January 2012)

B. 4413. The area of a symmetrical trapezium $\mathcal T$ is 4 units, it is not a rectangle, and it can be divided into four congruent trapezia that are similar to $\mathcal T$ . Determine the sides and angles of $\mathcal T$ .

(4 pont)

Deadline expired on February 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsük $\displaystyle \mathcal T$-nek egy hegyesszögü csúcsát. Ez meg kell egyezzen valamelyik kis trapéznak egy csúcsával. Ez csak úgy lehetséges, hogy a kis trapéznak e csúcsra illeszkedő oldalai $\displaystyle \mathcal T$-nek e csúcsra illeszkedő oldalain helyezkednek el. Ennek megfelelően a kis trapéz csak kétféleképpen helyezkedhet el, melyek közül az egyik állás $\displaystyle \mathcal T$ állásával megegyező, ebben az állásban a kis trapézt úgy kaphatjuk meg, hogy az adott csúcsból $\displaystyle \mathcal T$-t felére kicsinyítjük. Megmutatjuk, hogy egyik hegyeszögü csúcsnál sem lehet $\displaystyle \mathcal T$-vel megegyező állású kis trapéz.

Először is, nem lehet mindkét hegyeszögü csúcsnál $\displaystyle \mathcal T$-vel megegyező állású kis trapéz. Ebben az esetben ugyanis az első ábrán megjelölt 3 pont közül valamelyik kettő csúcsa kellene legyen a fennmaradó két kis trapéz közül ugyannak, ami nyilván nem lehetséges. Tegyük fel tehát, hogy az $\displaystyle A$ hegyesszögü csúcshoz $\displaystyle \mathcal T$-vel megegyező állású kis trapéz illeszkedik, a $\displaystyle B$ hegyesszögü csúcshoz viszont nem. Ekkor a két kis trapéz $\displaystyle X$-szel, illetve $\displaystyle Y$-nal jelölt csúcsa egybe kell hogy essen. Tegyük fel ugyanis, hogy $\displaystyle X\ne Y$. Jelölje a kis trapézok hosszabbik alapját $\displaystyle a$, szárát pedig $\displaystyle b$, ahol most $\displaystyle b<a$. Az $\displaystyle Y$ csúcshoz kell, hogy illeszkedjék egy harmadik kis trapéz, melynek egy $\displaystyle b$ hosszúságú oldala az $\displaystyle XY$ szakaszra esik. Innen $\displaystyle AD=2b\le a\le BC=AD$, vagyis $\displaystyle a=2b$ adódik, ami azt jelenti, hogy a három kis trapéz a második ábrán látható módon helyezkedik el. Mivel a fennmaradó rész nem is összefüggő, ez az eset tényleg nem fordulhat elő. Marad az $\displaystyle X=Y$ eset, amikor is $\displaystyle a=b$. Ekkor a $\displaystyle Z$ csúcshoz illeszkedő harmadik kis trapéz egyik $\displaystyle a$ hosszúságú oldala belsejében tartalmazza a $\displaystyle V$ pontot, ami azt jelenti, hogy az $\displaystyle UV$ szakasz mellé nem tudjuk odailleszteni a negyedik kis trapézt, lásd a harmadik ábrát.

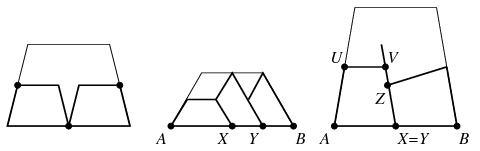
Beláttuk tehát, hogy $\displaystyle \mathcal T$-nek $\displaystyle A$ és $\displaystyle B$ csúcsához is $\displaystyle \mathcal T$-vel nem megegyező állású kis trapéz illeszkedik a negyedik ábra szerint. Nyilván $\displaystyle S\ne T$, és az is könnyen belátható, hogy $\displaystyle U=D$, $\displaystyle V=C$. Ellenkező esetben ugyanis az $\displaystyle X,Y,S,T,U,V,C,D$ csúcsok mindegyike egybe kellene essen a fennmaradó két kis trapéz valamelyik csúcsával, amiből következne, hogy az $\displaystyle U,V,C,D$ csúcsok ugyanannak a kis trapéznak csúcsai, a fennmaradó rész viszont egy konkáv hatszög lenne.

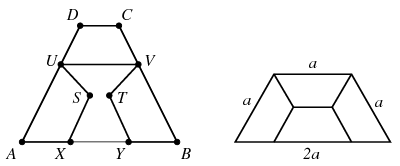
A felosztás tehát csak az ötödik ábra szerint lehetséges, ahonnan világos, hogy a trapéz szögei $\displaystyle 60$ és $\displaystyle 120$ fokosak. A trapéz oldalai $\displaystyle a,a,a,2a$ hosszúságúak, területe

$\displaystyle \frac{2a+a}{2}\cdot\frac{\sqrt{3}}{2}a=4,$

ahonnan $\displaystyle a=4/\root{4}\of{27}$.

Statistics:

109 students sent a solution.

4 points: Babik Bálint, Géczi Péter Attila, Janzer Barnabás, Jávorszky Natasa, Novák László, Papp Roland, Tardos Jakab, Varga 922 Dániel.

3 points: Ágoston Péter, Bingler Arnold, Csigi Máté, Czipó Bence, Di Giovanni Márk, Gyarmati Máté, Herczeg József, Kaprinai Balázs, Katona Dániel, Kecskés Boglárka, Leitereg Miklós, Lezsák Gábor, Maga Balázs, Mihálykó András, Viharos Andor, Zilahi Tamás.

2 points: 10 students.

1 point: 51 students.

0 point: 23 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, January 2012

109 students sent a solution.
4 points:	Babik Bálint, Géczi Péter Attila, Janzer Barnabás, Jávorszky Natasa, Novák László, Papp Roland, Tardos Jakab, Varga 922 Dániel.
3 points:	Ágoston Péter, Bingler Arnold, Csigi Máté, Czipó Bence, Di Giovanni Márk, Gyarmati Máté, Herczeg József, Kaprinai Balázs, Katona Dániel, Kecskés Boglárka, Leitereg Miklós, Lezsák Gábor, Maga Balázs, Mihálykó András, Viharos Andor, Zilahi Tamás.
2 points:	10 students.
1 point:	51 students.
0 point:	23 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?