Problem B. 4460. (May 2012)

B. 4460. Regular triangles ABD, BCE and CAF are drawn over the sides of a triangle ABC, on the outside. Let G and H denote the midpoints of the line segments BD and BE, respectively, and let the midpoint of triangle CAF be I. Prove that the lines AH, CG and BI are concurrent.

Suggested by Sz. Miklós, Herceghalom

(5 pont)

Deadline expired on June 11, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tegyük fel először, hogy a háromszög szögeire a szokásos jelölésekkel $\alpha$ , $\gamma$ <150^o és $\beta$ <120^o teljesül, vagyis a szóban forgó egyenesek az ábrának megfelelően részben a háromszög belsejében haladnak. Vezessük be még a

$HAC\sph=\alpha_1, BAH\sph=\alpha_2, IBA\sph=\beta_1, CBI\sph=\beta_2, GCB\sph=\gamma_1, ACG\sph=\gamma_2$

jelöléseket.

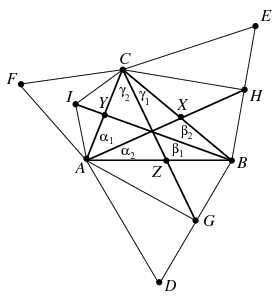
Az ACH, illetve ABH háromszögekre a szinusz-tételt felírva

$\frac{\sin\alpha_1}{\sin(\gamma+30^\circ)}=\frac{CH}{AH},\quad \frac{\sin\alpha_2}{\sin(\beta+60^\circ)}=\frac{BH}{AH},$

ahonnan

$\frac{\sin\alpha_1}{\sin\alpha_2}= \frac{\sin(\gamma+30^\circ)}{\sin(\beta+60^\circ)}\cdot \frac{CH}{BH}= \sqrt{3}\cdot\frac{\sin(\gamma+30^\circ)}{\sin(\beta+60^\circ)}.$

Hasonlóképpen kapjuk, hogy

$\frac{\sin\beta_1}{\sin\beta_2}= \frac{\sin(\alpha+30^\circ)}{\sin(\gamma+30^\circ)}\cdot \frac{AI}{CI}= \frac{\sin(\alpha+30^\circ)}{\sin(\gamma+30^\circ)}$

és

$\frac{\sin\gamma_1}{\sin\gamma_2}= \frac{\sin(\beta+60^\circ)}{\sin(\alpha+30^\circ)}\cdot \frac{BG}{AG}= \frac{1}{\sqrt{3}}\cdot\frac{\sin(\beta+60^\circ)}{\sin(\alpha+30^\circ)}.$

Következésképpen

$\frac{\sin\alpha_1}{\sin\alpha_2}\cdot\frac{\sin\beta_1}{\sin\beta_2}\cdot \frac{\sin\gamma_1}{\sin\gamma_2}=1.$

Most írjuk fel a szinusz-tételt az ACX és ABC háromszögekre, innen a

$\frac{\sin\alpha_1}{\sin\alpha_2}= \frac{\sin\gamma}{\sin\beta}\cdot \frac{XC}{BX}$

összefüggést kapjuk. Hasonlóképpen

$\frac{\sin\beta_1}{\sin\beta_2}= \frac{\sin\alpha}{\sin\gamma}\cdot \frac{YA}{CY}$

és

$\frac{\sin\gamma_1}{\sin\gamma_2}= \frac{\sin\beta}{\sin\alpha}\cdot \frac{ZB}{AZ}.$

Ezeket összeszorozva egyszerűsítés után

$\frac{XC}{BX}\cdot\frac{YA}{CY}\cdot\frac{ZB}{AZ}=1$

adódik, amivel a bizonyítandó állítást visszavezettük Ceva tételére.

Ha $\alpha$ =150^o, $\beta$ =120^o vagy $\gamma$ =150^o, akkor a fenti indoklás során 0-val is kellene osztanunk. Könnyen látható azonban, hogy ekkor a három egyenes rendre az A, B, illetve C csúcsban metszi egymást. Végül ha valamelyik szög túl nagy, akkor a fenti bizonyítás érvényben marad ha irányított szögekkel, illetve szakaszokkal dolgozunk; az $\alpha$ _i, $\beta$ _i, $\gamma$ _i szögek szinuszai közül és az AZ,ZB,BX,XC,CY,YA szakaszok hossza közül is pontosan kettő negatív lesz.

Statistics:

18 students sent a solution.

5 points: Bingler Arnold, Demeter Dániel, Forrás Bence, Herczeg József, Janzer Olivér, Kabos Eszter, Maga Balázs, Mester Márton, Ódor Gergely, Szabó 928 Attila.

4 points: Balogh Tamás, Sagmeister Ádám, Zsiros Ádám.

3 points: 3 students.

0 point: 2 students.

Problems in Mathematics of KöMaL, May 2012

18 students sent a solution.
5 points:	Bingler Arnold, Demeter Dániel, Forrás Bence, Herczeg József, Janzer Olivér, Kabos Eszter, Maga Balázs, Mester Márton, Ódor Gergely, Szabó 928 Attila.
4 points:	Balogh Tamás, Sagmeister Ádám, Zsiros Ádám.
3 points:	3 students.
0 point:	2 students.

Already signed up?
New to KöMaL?