Problem B. 4490. (November 2012)

B. 4490. P and Q are interior points on side AC of a non-isosceles triangle ABC such that $\angle ABP = \angle QBC< \frac 12\cdot \angle ABC$ . The interior angle bisectors drawn from A and C intersect the line segment BP at points K and L, and the line segment BQ at points M and N, respectively. Prove that the lines AC, KN and LM are concurrent.

Suggested by Sz. Miklós, Herceghalom

(6 pont)

Deadline expired on December 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Útmutatás: Menelaosz-tétel.

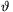Megoldás: A szokásos jelölések mellett legyen $ABP \sphericalangle = \vartheta$ . Mivel $\alpha$ $\ne$ $\gamma$ és $\alpha$ + $\gamma$ +2 $\vartheta$ < $\pi$ , a szögfelező-tétel és a szinusz-tétel szerint

$\frac{QN}{NB}=\frac{QC}{BC}=\frac{\sin\vartheta}{\sin(\gamma+\vartheta)}\ne \frac{\sin\vartheta}{\sin(\alpha+\vartheta)}=\frac{PA}{BA}=\frac{PK}{KB}.$

Ezért a KN egyenes nem párhuzamos az AC egyenessel, így azt egy X pontban metszi. Hasonlóképpen

$\frac{QM}{MB}=\frac{QA}{BA}= \frac{\sin(\beta-\vartheta)}{\sin(\gamma+\vartheta)}\ne \frac{\sin(\beta-\vartheta)}{\sin(\alpha+\vartheta)} =\frac{PC}{BC}=\frac{PL}{LB},$

így az LM egyenes az AC egyenest egy Y pontban metszi.

A Menelaosz-tételt a BPQ háromszögre alkalmazva

$\frac{PX}{XQ}\cdot\frac{QN}{NB}\cdot\frac{BK}{KP}=-1= \frac{PY}{YQ}\cdot\frac{QM}{MB}\cdot\frac{BL}{LP},$

ahol a PX,XQ, és ugyanúgy a PY,YQ irányított szakaszok közül is, az egyik hossza negatív. Mivel a fentiek szerint (itt mindegyik irányított szakasz hossza pozitív)

$\frac{QN}{NB}\cdot\frac{BK}{KP}= \frac{\sin(\alpha+\vartheta)}{\sin(\gamma+\vartheta)}= \frac{QM}{MB}\cdot\frac{BL}{LP}\ne 1,$

kapjuk, hogy PX:XQ=PY:YQ $\ne$ -1. Azon Z pontok mértani helye a síkon, melyekre a PZ:ZQ arány 1-től különböző állandó, egy olyan Apollóniusz-kör, mely elválasztja a P és Q pontokat. Ez a PQ egyenest két pontban metszi. Az irányításokat is figyelembe véve tehát X=Y, amint azt igazolni kellett.

Statistics:

29 students sent a solution.

6 points: Ágoston Péter, Balogh Tamás, Bogár Blanka, Fehér Zsombor, Fonyó Viktória, Gyulai-Nagy Szuzina, Herczeg József, Janzer Olivér, Kúsz Ágnes, Machó Bónis, Maga Balázs, Medek Ákos, Nagy Róbert, Petrényi Márk, Sagmeister Ádám, Szabó 789 Barnabás, Szabó 928 Attila, Szőke Tamás, Tardos Jakab, Tossenberger Tamás.

5 points: Bingler Arnold, Nagy-György Pál, Schultz Vera Magdolna, Williams Kada.

3 points: 1 student.

1 point: 2 students.

0 point: 2 students.

Problems in Mathematics of KöMaL, November 2012

29 students sent a solution.
6 points:	Ágoston Péter, Balogh Tamás, Bogár Blanka, Fehér Zsombor, Fonyó Viktória, Gyulai-Nagy Szuzina, Herczeg József, Janzer Olivér, Kúsz Ágnes, Machó Bónis, Maga Balázs, Medek Ákos, Nagy Róbert, Petrényi Márk, Sagmeister Ádám, Szabó 789 Barnabás, Szabó 928 Attila, Szőke Tamás, Tardos Jakab, Tossenberger Tamás.
5 points:	Bingler Arnold, Nagy-György Pál, Schultz Vera Magdolna, Williams Kada.
3 points:	1 student.
1 point:	2 students.
0 point:	2 students.

Already signed up?
New to KöMaL?