Problem B. 4517. (February 2013)

B. 4517. A $\ne$ B are interior points of the quadrant XY centred at O. The parallels drawn to the line OX through the points A, B intersect the radius OY at the points A_Y and B_Y. The lines drawn parallel to line OY intersect the radius OX at A_X and B_X. Determine the total area of the quadrilaterals AA_XB_XB and AA_YB_YB as a function of the length AB.

Suggested by Gy. Károlyi, Budapest, Brisbane

(4 pont)

Deadline expired on March 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: Használjunk szögfüggvényeket.

Megoldás. Legyen $AOA_X\sphericalangle=\alpha$ , $BOB_X\sphericalangle=\beta$ . Helyezzük el az ábrát a derékszögű koordinátarendszerben az ábra szerint, vizsgáljuk azt az esetet, amikor $\beta$ $\ge$ $\alpha$ .

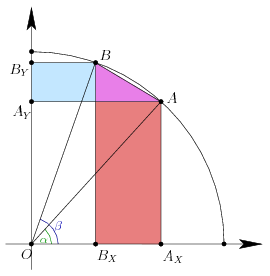
Az AA_XB_XB és a AA_YB_YB négyszög is trapéz. A területük összege

$t_{AA_XB_XB} + t_{AA_YB_YB} = \tfrac12 (AA_X+BB_X)\cdot A_XB_X + \tfrac12 (AA_Y+BB_Y)\cdot A_YB_Y =$

$= \tfrac12 (\sin\alpha+\sin\beta) \cdot (\cos\alpha-\cos\beta) + \tfrac12 (\cos\alpha+\cos\beta) \cdot (\sin\beta-\sin\alpha) =$

=cos $\alpha$ sin $\beta$ -sin $\alpha$ cos $\beta$ =sin ( $\beta$ - $\alpha$ ).

Az OAB egyenlő szárú háromszögből látható, hogy

$AB = 2 \sin\frac{\beta-\alpha}{2},$

amiből

$\sin(\beta-\alpha) = 2 \sin\frac{\beta-\alpha}2 \cos\frac{\beta-\alpha}2 = 2 \sin\frac{\beta-\alpha}2 \sqrt{1-\sin^2\frac{\beta-\alpha}2} = AB\cdot \sqrt{1-\frac{AB^2}4}.$

Tehát

$t_{AA_XB_XB} + t_{AA_YB_YB} = AB\cdot \sqrt{1-\frac{AB^2}4}.$

Statistics:

72 students sent a solution.

4 points: 60 students.

3 points: 7 students.

2 points: 2 students.

1 point: 3 students.

Problems in Mathematics of KöMaL, February 2013

72 students sent a solution.
4 points:	60 students.
3 points:	7 students.
2 points:	2 students.
1 point:	3 students.

Already signed up?
New to KöMaL?