Problem B. 4853. (February 2017)

B. 4853. Let \(\displaystyle K\) denote the centre of the incircle of a circumscribed quadrilateral \(\displaystyle ABCD\). \(\displaystyle M\) is a point on the line segment \(\displaystyle AK\), and \(\displaystyle N\) is a point on the line segment \(\displaystyle CK\), such that \(\displaystyle 2 MBN\sphericalangle= ABC\sphericalangle\). Prove that \(\displaystyle 2 MDN\sphericalangle=ADC\sphericalangle\).

(5 pont)

Deadline expired on March 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mivel \(\displaystyle K\) a beírt kör középpontja, ezért az \(\displaystyle AK\) és \(\displaystyle CK\) szakaszok szögfelezői a megfelelő \(\displaystyle BAD\) és \(\displaystyle BCD\) szögeknek.

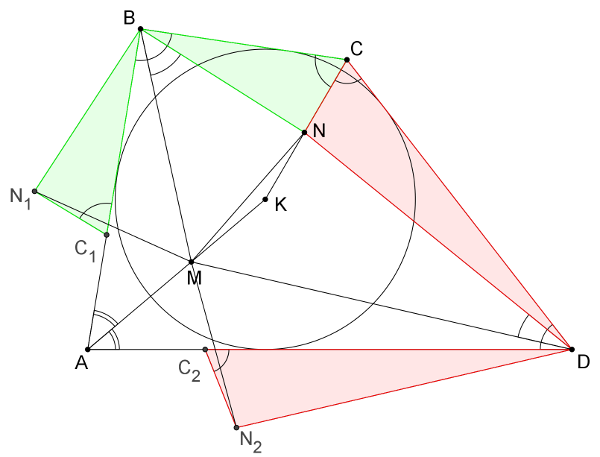
Feltehetjük, hogy \(\displaystyle AB≥BC\). Forgassuk el a \(\displaystyle BCN\) háromszöget a \(\displaystyle B\) pont körül úgy, hogy \(\displaystyle C\) pont képe, \(\displaystyle C_1\) az \(\displaystyle AB\) szakaszra essen. A kapott háromszög \(\displaystyle BC_1 N_1\).

Hasonlóan forgassuk el a \(\displaystyle DCN\) háromszöget a \(\displaystyle D\) pont körül úgy, hogy \(\displaystyle C\) pont képe, \(\displaystyle C_2\) az \(\displaystyle AD\) szakaszra essen. A kapott háromszög \(\displaystyle DC_2 N_2\).

\(\displaystyle BN=BN_1\), \(\displaystyle MBN∡=\frac12 ABC∡=ABM∡+CBN∡=ABM∡+C_1 BN_1∡=MBN_1∡\). Ezért a \(\displaystyle MBN\) és \(\displaystyle MBN_1\) háromszögek egybevágóak, mert megegyeznek két oldalban és a közbezárt szögben, hiszen az elforgatás miatt \(\displaystyle BN=BN_1\). Így \(\displaystyle MN=MN_1\).

Mivel az érintőnégyszög szemközti oldalainak összege egyenlő: \(\displaystyle AB+CD=AD+BC\), vagyis \(\displaystyle AB-BC=AD-CD\), ezért \(\displaystyle AC_1= AB-BC=AD-CD=AC_2\).

Ebből következik, hogy \(\displaystyle C_1\) és \(\displaystyle C_2\) szimmetrikus a \(\displaystyle BAD∡\) \(\displaystyle AM\) szögfelezőjére. Az elforgatások miatt \(\displaystyle C_1 N_1=CN=C_2 N_2\) és \(\displaystyle BC_1 N_1∡=BCN∡=DCN∡=DC_2 N_2∡\), ezért \(\displaystyle N_1\) és \(\displaystyle N_2\) is szimmetrikus az \(\displaystyle AM\) szögfelezőre. Emiatt \(\displaystyle MN_1=MN_2\). Így a fentieket figyelembe véve beláttuk, hogy \(\displaystyle MN=MN_2\), ami azt jelenti, hogy \(\displaystyle DMN\) és \(\displaystyle DMN_2\) háromszögek egybevágóak, mert mindhárom oldaluk megegyezik. Ebből következik, hogy \(\displaystyle MDN∡=MDN_2∡=ADM∡+C_2 DN_2∡=ADM∡+CDN∡=ADC∡-MDN∡\), vagyis \(\displaystyle MDN∡=ADC∡-MDN∡\).

Rendezve: \(\displaystyle ADC∡=2\cdot MDN∡\), vagyis \(\displaystyle MDN∡=\frac12 ADC∡\). Ezt kellett belátnunk.

Statistics:

20 students sent a solution.
5 points:	Baran Zsuzsanna, Borbényi Márton, Csahók Tímea, Gáspár Attila, Kerekes Anna, Kocsis Júlia, Kővári Péter Viktor, Márton Dénes, Schrettner Jakab, Szabó 417 Dávid, Szemerédi Levente, Tóth Viktor, Velkey Vince.
4 points:	Szabó Kristóf, Szécsényi Nándor, Tiderenczl Dániel.
3 points:	1 student.
0 point:	3 students.

Problems in Mathematics of KöMaL, February 2017