Problem B. 4889. (September 2017)

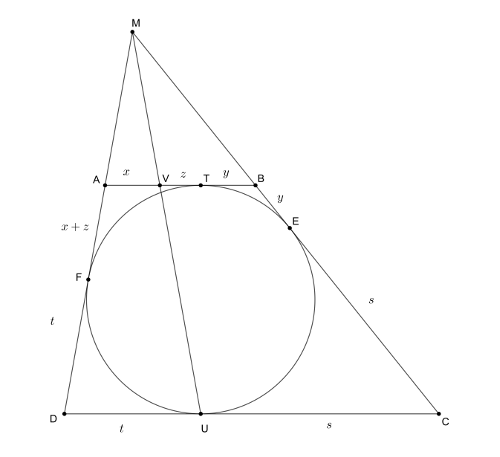
B. 4889. The trapezium \(\displaystyle ABCD\) has an inscribed circle. The circle touches base \(\displaystyle AB\) at point \(\displaystyle T\), and the parallel base \(\displaystyle CD\) at point \(\displaystyle U\). Let \(\displaystyle M\) denote the intersection of the lines of legs \(\displaystyle AD\) and \(\displaystyle BC\), and let \(\displaystyle V\) be the intersection of side \(\displaystyle AB\) with line \(\displaystyle MU\). Show that \(\displaystyle AT=VB\).

(4 pont)

Deadline expired on October 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Legyen \(\displaystyle AV=x\), \(\displaystyle VT=z\), \(\displaystyle TB=BE=y\), \(\displaystyle FD=DU=t\), \(\displaystyle UC=CE=s\), \(\displaystyle AF=AT=x+z\). A beírt kör átmérőjének négyzete Pitagorasz tétele szerint \(\displaystyle (x+z+t)^2 - (x+z-t)^2 = (s+y)^2 - (s-y)^2\), amiből \(\displaystyle \dfrac{x+z}{s}=\dfrac{y}{t}\). A párhuzamos szelők tételéből pedig \(\displaystyle \dfrac{x}{t}=\dfrac{y+z}{s}\). E két utóbbi egyenlőséget összeszorozva: \(\displaystyle \dfrac{x(x+z)}{st}=\dfrac{y(y+z)}{st}\), \(\displaystyle x^2-y^2 + z(x-y)=0\), \(\displaystyle (x-y)(x+y+z)=0\), azaz \(\displaystyle x=y\), így \(\displaystyle AT=x+z= y+z= VB\).

Statistics:

90 students sent a solution.
4 points:	57 students.
3 points:	21 students.
2 points:	2 students.
1 point:	3 students.
0 point:	7 students.

Problems in Mathematics of KöMaL, September 2017