 |
A B. 4891. feladat (2017. szeptember) |
B. 4891. Az \(\displaystyle S_1\), \(\displaystyle S_2\), \(\displaystyle S_3\) körök páronként kívülről érintik egymást. Legyenek \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) rendre az \(\displaystyle S_1\) és \(\displaystyle S_2\), \(\displaystyle S_1\) és \(\displaystyle S_3\), \(\displaystyle S_2\) és \(\displaystyle S_3\) körök közös pontjai. Az \(\displaystyle AB\) egyenes ismételten elmetszi az \(\displaystyle S_2\) és \(\displaystyle S_3\) köröket a \(\displaystyle D\), illetve az \(\displaystyle E\) pontokban. A \(\displaystyle DC\) egyenes újabb metszéspontja az \(\displaystyle S_3\) körrel legyen az \(\displaystyle F\) pont. Bizonyítsuk be, hogy a \(\displaystyle DEF\) háromszög derékszögű.
(Kvant)
(5 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldásvázlat. Azt fogjuk belátni, hogy \(\displaystyle DEF\sphericalangle =90^{\circ}\). A \(\displaystyle B, E, F\) és \(\displaystyle C\) pontok az \(\displaystyle S_{3}\) kör pontjai, a \(\displaystyle BEFC\) húrnégyszög, tehát elegendő belátni, hogy a \(\displaystyle BCD\sphericalangle\) derékszög.
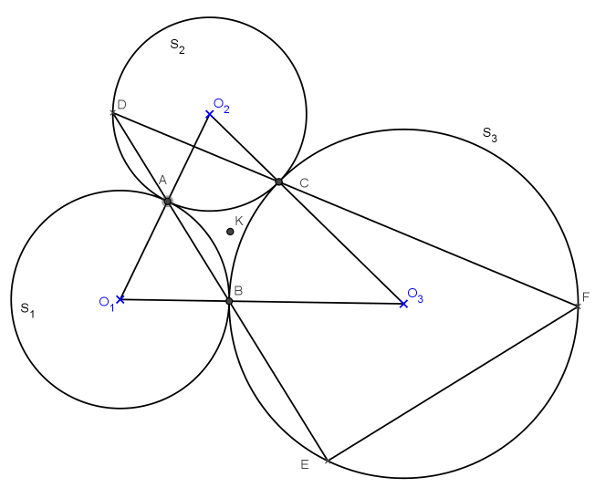
Legyen az \(\displaystyle S_1\), \(\displaystyle S_2\) és \(\displaystyle S_3\) körök középpontja \(\displaystyle O_1\), \(\displaystyle O_2\) és \(\displaystyle O_3\).
Az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) érintési pontok, tehát rajta vannak rendre az \(\displaystyle O_1O_2\), \(\displaystyle O_1O_3\) és \(\displaystyle O_2O_3\) szakaszokon. \(\displaystyle AO_1=BO_1\), \(\displaystyle BO_3=CO_3\) és \(\displaystyle CO_2=AO_2\), ami azt jelenti, hogy \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) egyben az \(\displaystyle O_1O_2O_3\) háromszög beírt körének érintési pontjai. A beírt kör középpontja legyen \(\displaystyle K\). Az \(\displaystyle O_1O_2O_3\) háromszög szögei pedig \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\). Az egyenlő szárú háromszögekből azonnal számolhatóak az \(\displaystyle ABC\) háromszög szögei is: \(\displaystyle ABC\sphericalangle=\frac{\alpha+\gamma}{2}\), \(\displaystyle BCA\sphericalangle=\frac{\beta+\gamma}{2}\), \(\displaystyle CAB\sphericalangle=\frac{\beta+\alpha}{2}\)
Most alkalmazzuk az \(\displaystyle S_2\) körben a kerületi-középponti szögek tételét:
\(\displaystyle ADC\sphericalangle=\frac{AO_2C\sphericalangle}{2}=\frac{\beta}{2}.\)
\(\displaystyle DCB\sphericalangle=180°-ADC\sphericalangle-ABC\sphericalangle=180°-\frac{\alpha+\beta+\gamma}{2}=90°,\)
ezért \(\displaystyle DEF\sphericalangle\) is derékszög.
Statisztika:
112 dolgozat érkezett. 5 pontot kapott: 89 versenyző. 4 pontot kapott: 7 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 6 versenyző.
A KöMaL 2017. szeptemberi matematika feladatai

