A B. 4896. feladat (2017. október)

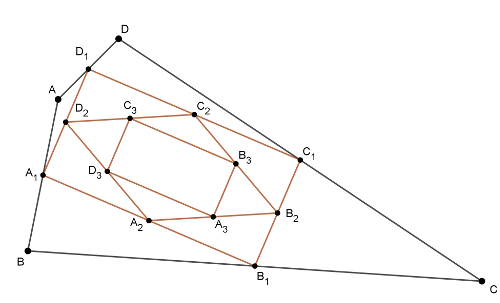
B. 4896. Az \(\displaystyle ABCD\) konvex négyszög oldalfelező pontjai legyenek \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), \(\displaystyle D_1\). Az \(\displaystyle A_1B_1C_1D_1\) négyszög oldalfelező pontjai legyenek \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\), \(\displaystyle D_2\) és ezt folytatjuk tovább. Bizonyítsuk be, hogy ha \(\displaystyle A_1B_1C_1D_1\) húrnégyszög, akkor \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is húrnégyszög.

Javasolta: Szoldatics József (Budapest)

(3 pont)

A beküldési határidő 2017. november 10-én LEJÁRT.

Megoldás. Ismert, hogy egy négyszög oldalfelező pontjai paralelogrammát alkotnak. Tudjuk, hogy ez a paralelogramma, \(\displaystyle A_1B_1C_1D_1\) húrnégyszög, így tehát téglalap. Egy téglalap oldalfelező pontjai rombuszt határoznak meg, tehát \(\displaystyle A_2B_2C_2D_2\) rombusz. Egy rombusz oldalfelező pontjai ismét téglalapot alkotnak, és így tovább: \(\displaystyle A_{2k}B_{2k}C_{2k}D_{2k}\) mindig rombusz, míg \(\displaystyle A_{2k+1}B_{2k+1}C_{2k+1}D_{2k+1}\) mindig téglalap. Tehát \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is téglalap, ami azt jelenti, hogy húrnégyszög is.

Statisztika:

122 dolgozat érkezett.
3 pontot kapott:	97 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2017. októberi matematika feladatai