Problem B. 4896. (October 2017)

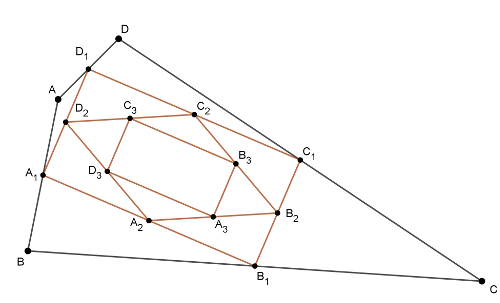
B. 4896. Let \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), \(\displaystyle D_1\) denote the midpoints of the sides of a convex quadrilateral \(\displaystyle ABCD\). Let \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\), \(\displaystyle D_2\) denote the midpoints of the sides of the quadrilateral \(\displaystyle A_1B_1C_1D_1\). The procedure is continued. Prove that if quadrilateral \(\displaystyle A_1B_1C_1D_1\) is cyclic then quadrilateral \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is also cyclic.

Proposed by J. Szoldatics, Budapest

(3 pont)

Deadline expired on November 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ismert, hogy egy négyszög oldalfelező pontjai paralelogrammát alkotnak. Tudjuk, hogy ez a paralelogramma, \(\displaystyle A_1B_1C_1D_1\) húrnégyszög, így tehát téglalap. Egy téglalap oldalfelező pontjai rombuszt határoznak meg, tehát \(\displaystyle A_2B_2C_2D_2\) rombusz. Egy rombusz oldalfelező pontjai ismét téglalapot alkotnak, és így tovább: \(\displaystyle A_{2k}B_{2k}C_{2k}D_{2k}\) mindig rombusz, míg \(\displaystyle A_{2k+1}B_{2k+1}C_{2k+1}D_{2k+1}\) mindig téglalap. Tehát \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is téglalap, ami azt jelenti, hogy húrnégyszög is.

Statistics:

122 students sent a solution.
3 points:	97 students.
2 points:	7 students.
1 point:	14 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, October 2017