Problem B. 4908. (November 2017)

B. 4908. Let \(\displaystyle C\) denote an arbitrary point on the circumference of a circle of diameter \(\displaystyle AB\). Let \(\displaystyle T\) be the perpendicular projection of point \(\displaystyle C\) onto the line segment \(\displaystyle AB\). Draw the circle of centre \(\displaystyle C\) that passes through \(\displaystyle T\). Let the intersections of the two circles be \(\displaystyle P\) and \(\displaystyle Q\). Prove that line \(\displaystyle PQ\) bisects the line segment \(\displaystyle CT\).

(Kvant)

(4 pont)

Deadline expired on December 11, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle AB\) és \(\displaystyle CD\) két egymást metsző húr a \(\displaystyle k\) körben (1. ábra).

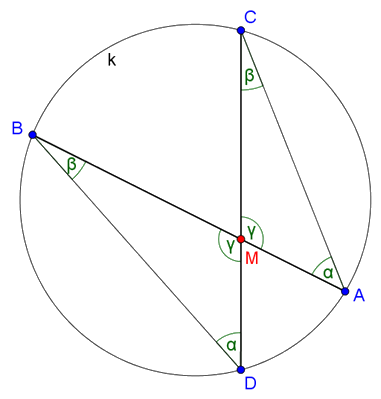
1. ábra

Az \(\displaystyle AMC\) és \(\displaystyle BMD\) háromszögek hasonlóságát felhasználva:

\(\displaystyle \frac{AM}{CM}=\frac{DM}{BM}.\)

Átszorozva: \(\displaystyle AM\cdot BM=CM\cdot DM\).

Tehát adott körben két egymást metsző húr esetén a húrdarabok szorzata egyenlő.

Alkalmazzuk ezt az összefüggést a feladatban szereplő körökre. Használjuk a 2. ábra jelöléseit.

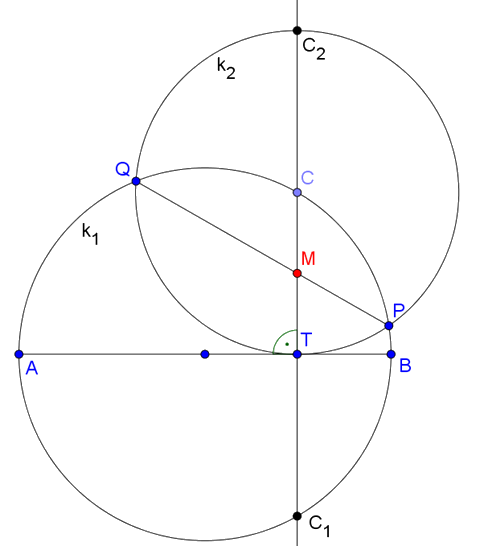
2. ábra

Legyen \(\displaystyle C\) az \(\displaystyle A\) és \(\displaystyle B\) ponttól különböző pontja a \(\displaystyle k_1\) körnek. A \(\displaystyle CM\) egyenes \(\displaystyle k_1\) és \(\displaystyle k_2\) körrel való második metszéspontjai legyenek \(\displaystyle C_1\) és \(\displaystyle C_2\). Az \(\displaystyle AB\) átmérő felezi a rá merőleges \(\displaystyle CC_1\) húrt, ezért \(\displaystyle CT= C_1 T\). \(\displaystyle CT\) és \(\displaystyle C_2 C\) sugár a \(\displaystyle k_2\) körben, így \(\displaystyle C_2 C= CT= C_1 T\).

Alkalmazzuk a húrdarabokra vonatkozó összefüggést először a \(\displaystyle k_1\) körben a \(\displaystyle PQ\) és \(\displaystyle CC_1\) húrokra:

\(\displaystyle PM\cdot QM=CM\cdot C_1 M;\)

majd a \(\displaystyle k_2\) körben a \(\displaystyle PQ\) és \(\displaystyle TC_2\) húrokra:

\(\displaystyle PM\cdot QM=TM\cdot C_2 M.\)

Ebből látszik, hogy

\(\displaystyle CM\cdot C_1 M=TM\cdot C_2 M,\)

\(\displaystyle CM\cdot(C_1 T+TM)= TM\cdot (C_2 C+CM).\)

Mivel \(\displaystyle C_1 T=CT\) és \(\displaystyle C_2 C= CT\), így (felhasználva, hogy bármely szakasz hossza pozitív):

\(\displaystyle CM\cdot(CT+TM)= TM\cdot(CT+CM),\)

\(\displaystyle CM\cdot CT= TM\cdot CT.\)

Tehát \(\displaystyle CM= TM\), vagyis a \(\displaystyle PQ\) egyenes felezi a \(\displaystyle CT\) szakaszt.

Ha a \(\displaystyle C\) pont egybeesik az \(\displaystyle A\) vagy \(\displaystyle B\) ponttal, akkor a \(\displaystyle T\) pont is oda esik, így a \(\displaystyle CT\) szakasz egy pont lesz.

Jánosik Máté (Győr, Révai Miklós Gimn., 8. évf) dolgozata alapján

Statistics:

61 students sent a solution.
4 points:	Ajtai Boglárka, Apagyi Dávid, Beke Csongor, Busa 423 Máté, Csépányi István, Csiszár Zoltán, Daróczi Sándor, Dobák Dániel, Dózsa Ferenc, Döbröntei Dávid Bence, Fitos Bence, Fraknói Ádám, Fülöp Anna Tácia, Geretovszky Anna, Győrffy Ágoston, Harsányi Benedek, Hervay Bence, Hordós Adél Zita, Jánosik Áron, Jánosik Máté, Kerekes Anna, Kocsis Anett, Kovács 654 Áron , Kupás Vendel Péter, Lukács Lilla Réka, Markó Anna Erzsébet, Márton Dénes, Mészáros Anna, Mikulás Zsófia, Molnár-Sáska Zoltán, Olosz Adél, Osztényi József, Pituk Gábor, Richlik Róbert, Riedel Zsuzsanna, Schifferer András, Schneider Anna, Schrettner Jakab, Shuborno Das, Szabó 417 Dávid, Szabó 864 Blanka, Szabó 997 Balázs István, Szemerédi Levente, Szinyéri 427 Bence, Tiderenczl Dániel, Velkey Vince, Weisz Máté, Williams Hajna, Zólomy Kristóf, Zsigri Bálint.
3 points:	3 students.
2 points:	1 student.
1 point:	3 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, November 2017