 Problem B. 4919. (December 2017)
Problem B. 4919. (December 2017)
B. 4919. Let \(\displaystyle I\) be the centre of the inscribed circle of triangle \(\displaystyle ABC\). The inscribed circle touches the sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at the points \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\), respectively. The lines \(\displaystyle AB\) and \(\displaystyle A_1B_1\) intersect at point \(\displaystyle K\). Show that the circle centred at \(\displaystyle K\) and passing through \(\displaystyle C_1\), and the inscribed circles of the kites \(\displaystyle AC_1IB_1\) and \(\displaystyle BA_1IC_1\) have a tangent in common, and that tangent passes through the point \(\displaystyle C\).
(6 pont)
Deadline expired on January 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje az \(\displaystyle ABC\) háromszög, az \(\displaystyle AC_1IB_1\) deltoid, illetve a \(\displaystyle BA_1IC_1\) deltoid beírt körét rendre \(\displaystyle \omega\), \(\displaystyle \omega_a\), illetve \(\displaystyle \omega_b\); a \(\displaystyle K\) középpontú, \(\displaystyle C_1\)-en átmenő kört \(\displaystyle \Omega\), a \(\displaystyle C\) középpontú, \(\displaystyle A_1\)-en és \(\displaystyle B_1\)-en átmenő kört \(\displaystyle \gamma\). Az \(\displaystyle \omega_a\) és \(\displaystyle \omega_b\) középpontja legyen \(\displaystyle P\), illetve \(\displaystyle Q\). Az \(\displaystyle AC_1IB_1\) és \(\displaystyle BA_1IC_1\) deltoidoknak az \(\displaystyle A_1,B_1,C_1\) csúcsoknál derékszöge van, a beírt körük a szögfelezőik metszéspontja. Ezért az ábrán megjelölt szögek \(\displaystyle 45^\circ\)-osak.
Először megmutatjuk, hogy a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle K\) pontok egy egyenesre esnek. Ehhez a Menelaosz-tétel megfordítását fogjuk az \(\displaystyle ABI\) háromszögre alkalmazni.
A Menelaosz-tételt az \(\displaystyle ABC\) háromszögre és a \(\displaystyle KA_1B_1\) egyenesre felírva \(\displaystyle \frac{AK}{KB}\cdot\frac{BA_1}{A_1C}\cdot\frac{CB_1}{B_1A}=-1\), amiből
\(\displaystyle \frac{AK}{KB} = -\frac{A_1C}{BA_1}\cdot\frac{B_1A}{CB_1} = -\frac{AC_1}{C_1B}. \)
A szögfelezőtételt alkalmazva az \(\displaystyle AC_1I\) és \(\displaystyle IC_1B\) háromszögekben,
\(\displaystyle \frac{BQ}{QI}=\frac{C_1B}{C_1I} \quad\text{és}\quad \frac{IP}{PA}=\frac{C_1I}{AC_1}. \)
Ezeket beírva,
\(\displaystyle \frac{AK}{KB}\cdot\frac{BQ}{QI}\cdot\frac{IP}{PA} = \left(-\frac{AC_1}{C_1B}\right) \cdot\frac{C_1B}{C_1I} \cdot\frac{C_1I}{AC_1} = -1. \)
A Menelaosz-tétel megfordítása biztosítja, hogy az \(\displaystyle ABI\) háromszögben a \(\displaystyle K,P,Q\) pontok valóban egy egyenesen vannak.
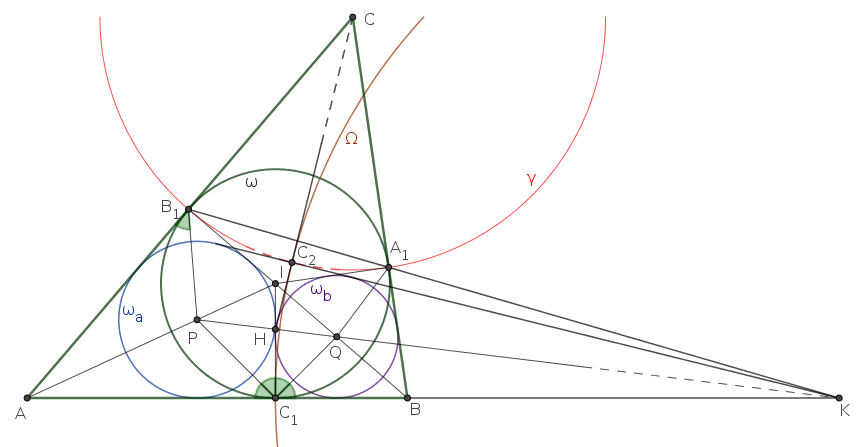
Az \(\displaystyle \omega_a\), \(\displaystyle \omega_b\) és \(\displaystyle \Omega\) köröknek a \(\displaystyle C_1I\) egyenes közös érintője. A másik közös érintőt úgy kaphatjuk, hogy az \(\displaystyle C_1I\) egyenest tükrözzük a \(\displaystyle PQK\) centrálisra. Legyen \(\displaystyle PQ\) és \(\displaystyle C_1I\) metszéspontja \(\displaystyle H\), és legyen \(\displaystyle C_2\) a \(\displaystyle C_1\) tükörképe a \(\displaystyle PQK\) egyenesre. Ekkor tehát \(\displaystyle HC_2\) a másik közös érintője az \(\displaystyle \omega_a\), \(\displaystyle \omega_b\) és \(\displaystyle \Omega\) köröknek, és azt kell igazolnunk, hogy a \(\displaystyle HC_2\) egyenes a \(\displaystyle C\) ponton is átmegy. Ehhez előbb azt mutatjuk meg, hogy \(\displaystyle C_2\) rajta van a \(\displaystyle \gamma\) körön.
Legyen \(\displaystyle \alpha=BAC\sphericalangle\) és \(\displaystyle \beta=CBA\sphericalangle\). A \(\displaystyle PC_1C_2\) és \(\displaystyle PC_2B_1\) egyenlő szárú háromszögek, valamint az \(\displaystyle AC_1PB_1\) négyszög szögeinek összeszámolásából kapjuk, hogy
\(\displaystyle B_1C_2C_1\sphericalangle = B_1C_2P\sphericalangle + PC_2C_1\sphericalangle = (90^\circ-\tfrac12 C_2PB_1\sphericalangle)+(90^\circ-\tfrac12 C_1PC_2\sphericalangle)= \)
\(\displaystyle = 180^\circ-\tfrac12C_1PB_1\sphericalangle = 180^\circ -\tfrac12(C_1AB_1\sphericalangle+AB_1P\sphericalangle+PC_1A\sphericalangle) = \)
\(\displaystyle = 180^\circ -\tfrac12(45^\circ+\alpha+45^\circ) = 135^\circ-\frac\alpha2. \)
Hasonlóan latjuk, hogy \(\displaystyle C_1C_2A_1\sphericalangle=135^\circ-\frac\beta2\), így
\(\displaystyle A_1C_2B_1\sphericalangle= 360^\circ-B_1C_2C_1\sphericalangle-C_1C_2A_1\sphericalangle= 90^\circ+\frac{\alpha+\beta}2=180^\circ-\tfrac12 B_1CA_1\sphericalangle. \)
A kerületi és középponti szögek tételének megfordítása szerint ebből következik, hogy a \(\displaystyle \gamma\) kör átmegy a \(\displaystyle C_2\) ponton.
Már csak annak igazolása van hátra, hogy a \(\displaystyle HC_2\) egyenes átmegy a \(\displaystyle C\) csúcson. A \(\displaystyle K\) pontnak a \(\displaystyle \omega\) körre vonatkozó hatványából
\(\displaystyle KC_2^2 = KC_1^2 = KA_1\cdot KB_1; \)
A \(\displaystyle \gamma\)-ra vonatkozó hatvány szerint ez azt jelenti, hogy a \(\displaystyle KC_2\) egyenes a \(\displaystyle C_2\) pontban érinti a \(\displaystyle \gamma\) kört. Így a \(\displaystyle \gamma\) kör \(\displaystyle CC_2\) sugara merőleges a \(\displaystyle KC_2\) érintőre. De a tükrözés miatt \(\displaystyle HC_2K\sphericalangle=KC_1H\sphericalangle=90^\circ\), tehát \(\displaystyle HC_2\) is merőleges \(\displaystyle KC_2\)-re. A \(\displaystyle HC_2\) és \(\displaystyle CC_2\) szakasz is merőleges \(\displaystyle KC_2\), ami bizonyítja azt, hogy a \(\displaystyle HC_2\) egyenes valóban átmegy \(\displaystyle C\)-n.
Statistics:
16 students sent a solution. 6 points: Daróczi Sándor, Döbröntei Dávid Bence, Fekete Richárd, Gáspár Attila, Geretovszky Anna, Janzer Orsolya Lili, Kerekes Anna, Pituk Gábor, Schrettner Jakab, Szabó 417 Dávid, Szabó 997 Balázs István, Weisz Máté, Zólomy Kristóf. 5 points: Shuborno Das. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, December 2017
