 |
A B. 4920. feladat (2017. december) |
B. 4920. Hányféleképpen lehet \(\displaystyle 1\times2\)-es dominókkal átfedés és hézag nélkül lefedni a \(\displaystyle 8\times8\)-as sakktábla körül felvett 2 egység szélességű szegélyt? (Az ábrán látható két lefedést különbözőnek tekintjük.)
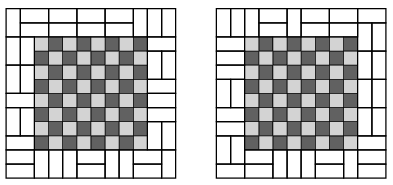
Javasolta: Róka Sándor (Nyíregyháza)
(6 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. A megoldás során felhasználjuk azt a jól ismert állítást, hogy egy \(\displaystyle 2\times n\)-es téglalapot \(\displaystyle 1\times 2\)-es dominókkal \(\displaystyle F_{n+1}\)-féleképpen lehet hézagmentesen és átfedések nélkül lefedni, vagyis parkettázni, ahol \(\displaystyle F_{n+1}\) a Fibonacci-sorozat \(\displaystyle (n+1)\)-edik tagja. (A Fibonacci-sorozatot az \(\displaystyle F_0=0,F_1=1\), és \(\displaystyle n\geq 2\)-re \(\displaystyle F_n=F_{n-1}+F_{n-2}\) rekurzió határozza meg. A hivatkozott állítás indukcióval könnyen igazolható. Ha \(\displaystyle n=1\), akkor valóban \(\displaystyle F_2=1\) lehetőség, ha pedig \(\displaystyle n=2\), akkor valóban \(\displaystyle F_3=2\) lehetőség van. Ha most \(\displaystyle n\geq 3\), akkor a \(\displaystyle 2\times n\)-es táblázat bal szélén vagy egy függőlegesen álló dominó van, és ezesetben a tőle jobbra lévő \(\displaystyle 2\times (n-1)\)-es részt kell lefednünk, ami \(\displaystyle F_n\)-féleképpen tehető meg, vagy pedig két vízszintesen álló dominó van egymás alatt a bal szélén, és ekkor a tőlük jobbra lévő \(\displaystyle 2\times (n-2)\)-es részt kell lefednünk, ami \(\displaystyle F_{n-1}\)-féleképpen tehető meg. így a lehetőségek száma valóban \(\displaystyle F_{n}+F_{n-1}=F_{n+1}\).)
Először tekintsük azokat a parkettázásokat, amikor a bal felső mezőt egy vízszintesen álló dominó fedi le. Világos, hogy így a parkettázások felét fogjuk megszámolni (a bal felső és a jobb alsó sarkot összekötő átlóra tükrözve kapjuk ezekből azokat, melyeknél a bal felső mezőt függőlegesen álló dominó fedi).
Ha a bal felső \(\displaystyle 2\times 2\)-es négyzet jobb szélén lévő piros vonal egy dominót kettévág, akkor a fedés onnan egyértelműen folytatható, és befejezhető az 1. ábra szerint.
Tegyük most fel, hogy a bal felső \(\displaystyle 2\times 2\)-es rész jobb szélén lévő piros vonal nem vág ketté dominót. Két esetet különböztetünk meg aszerint, hogy a jobb alsó sarkot vízszintes vagy függőleges dominó fedi.
1. eset. Tegyük fel először, hogy vízszintes. Ekkor a jobb alsó \(\displaystyle 2\times 2\)-es négyzet bal szélén lévő piros vonal sem vág ketté dominót, hiszen különben az 1. ábra szerinti parkettázást kapnánk. A bal alsó \(\displaystyle 2\times 2\)-es négyzet felső oldalán lévő vonal
vagy nem vág ketté dominót (2. ábra),
vagy kettőt is kettévág (3. ábra),
hiszen a vonal feletti \(\displaystyle 9\times 2\)-es részt különben nem lehetne lefedni. Utóbbi esetben a bal alsó sarkot egy vízszintes dominónak kell fednie. Az első esetben egy \(\displaystyle 9\times 2\)-es és egy \(\displaystyle 2\times 10\)-es részt kell lefedni dominókkal, ez \(\displaystyle F_{10}F_{11}\)-féleképpen tehető meg. A második esetben pedig egy \(\displaystyle 8\times 2\)-es és egy \(\displaystyle 2\times 8\)-as téglalapot kell lefedni dominókkal, ez \(\displaystyle F_{9}^2\)-féleképpen tehető meg. Az ábra szimmetriáját kihasználva a felső és jobb oldali sáv által alkotott L alakú rész lefedésére ugyanennyi, vagyis \(\displaystyle F_{10}F_{11}+F_{9}^2\) féle lehetőség van. összesen tehát az 1. esetben a parkettázások száma \(\displaystyle (F_{10}F_{11}+F_{9}^2)^2\).
2. eset. Most tegyük fel, hogy a jobb alsó sarkot függőleges dominó fedi. A jobb alsó \(\displaystyle 2\times 2\)-es négyzet felső oldala nem vághat ketté dominót, mert akkor a fedés egyértelmű befejezésében a bal felső sarkot is függőleges dominónak kellene fednie. Tehát ismét kialakul két L alakú sáv, ahol az 1. esetben látott esetszétválasztáshoz hasonlóan megszámolhatjuk a fedéseket. Az alsó L fedésére \(\displaystyle F_{10}F_{12}+F_9F_{10}\) lehetőség van (4. és 5. ábra szerinti esetek alapján), a felső L fedésére pedig \(\displaystyle F_{11}F_{9}+F_9F_8\). így a 2. esetben a lehetőségek száma \(\displaystyle (F_{10}F_{12}+F_9F_{10})(F_{11}F_{9}+F_9F_8)\).
Tehát feltéve, hogy a bal felső sarkot vízszintes dominó fedi, a lehetőségek száma \(\displaystyle 1+(F_{10}F_{11}+F_{9}^2)^2+(F_{10}F_{12})(F_{11}F_{9}+F_9F_8)\), így a feladat kérdésére a válasz ennek kétszerese, vagyis:
\(\displaystyle 2(1+(F_{10}F_{11}+F_{9}^2)^2+(F_{10}F_{12}+F_9F_{10})(F_{11}F_{9}+F_9F_8))=146458404.\)
Megjegyzés. A válasz \(\displaystyle 4(2F_{10}^2+1)^2\) alakban is írható.
Statisztika:
84 dolgozat érkezett. 6 pontot kapott: Argay Zsolt, Baski Bence, Beke Csongor, Csányi Dávid, Csaplár Viktor, Daróczi Sándor, Dobák Dániel, Fitos Bence, Fraknói Ádám, Füredi Erik Benjámin, Gáspár Attila, Gyetvai Miklós, Gyimesi Péter, Győrffy Ágoston, Győrffy Johanna, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Jánosik Máté, Jedlovszky Pál, Kántor András Imre, Kerekes Anna, Kiss Gergely, Kitschner Bernadett, Kulcsár Gergely, Márton Dénes, Mikulás Zsófia, Miszler Levente, Molnár-Sáska Zoltán, Nagy Nándor, Noszály Áron, Pituk Gábor, Póta Balázs, Reimann Kristóf, Saár Patrik, Soós 314 Máté, Szabó 417 Dávid, Szabó 864 Blanka, Vári-Kakas Andor, Velich Nóra, Weisz Máté. 5 pontot kapott: Bencsik Ádám, Biczó Benedek, Fülöp Anna Tácia, Janzer Orsolya Lili, Molnár Bálint, Tiszay Ádám, Zsigri Bálint. 4 pontot kapott: 17 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. decemberi matematika feladatai

