 Problem B. 4923. (January 2018)
Problem B. 4923. (January 2018)
B. 4923. The interior angle bisector drawn from vertex \(\displaystyle A\) of triangle \(\displaystyle ABC\) intersects side \(\displaystyle BC\) at \(\displaystyle E\), and the interior angle bisector drawn from vertex \(\displaystyle B\) intersects side \(\displaystyle AC\) at \(\displaystyle F\). Let \(\displaystyle O\) denote the centre of the inscribed circle of the triangle. What may be the size of the angle at \(\displaystyle C\) if the sum of the areas of \(\displaystyle \triangle OFA\) and \(\displaystyle \triangle OBE\) equals the area of \(\displaystyle \triangle AOB\)?
(3 pont)
Deadline expired on February 12, 2018.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Használjuk az ábra jelöléseit. A beírt kör sugara legyen \(\displaystyle r\).
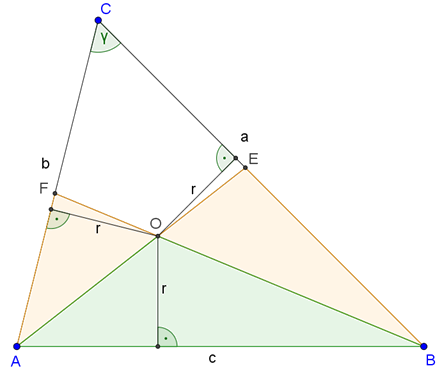
A szögfelező tételt felhasználva:
\(\displaystyle AF=b\cdot \frac{c}{a+c}\mathrm{~és~} BE=a\cdot \frac{c}{b+c}.\)
\(\displaystyle T_{AOB}=c\cdot \frac r2,\)
\(\displaystyle T_{OFA}=AF\cdot \frac r2=\frac{b}{a+c}\cdot c\cdot\frac r2,\)
\(\displaystyle T_{OBE}=BE\cdot \frac r2=\frac{a}{b+c}\cdot c\cdot\frac r2.\)
\(\displaystyle T_{AOB}=T_{OFA}+T_{OBE},\)
vagyis
\(\displaystyle c\cdot \frac r2=\frac{b}{a+c}\cdot c\cdot\frac r2+\frac{a}{b+c}\cdot c\cdot\frac r2.\)
Leosztva \(\displaystyle c\cdot \frac r2≠0\)-val:
\(\displaystyle 1=\frac{b}{a+c}+\frac{a}{b+c}.\)
Közös nevezőre hozva:
\(\displaystyle 1=\frac{b(b+c)+a(a+c)}{(a+c)(b+c)}.\)
Szorozzuk be mindkét oldalt az \(\displaystyle (a+c)(b+c)>0\) kifejezéssel és bontsuk fel a zárójeleket:
\(\displaystyle ab+ac+bc+c^2=b^2+bc+a^2+ac.\)
Rendezve:
\(\displaystyle c^2=a^2+b^2-ab.\)
Felhasználva a koszinusz-tételt:
\(\displaystyle c^2=a^2+b^2-2ab\cos γ=a^2+b^2-ab,\)
vagyis \(\displaystyle \cos γ=1/2\). Mivel \(\displaystyle 0<γ<180°\), így csak \(\displaystyle γ=60°\) lehet a háromszög \(\displaystyle C\) csúcsnál lévő szöge. Az átalakítások ekvivalensek voltak, tehát \(\displaystyle γ=60°\)esetén telesül a háromszögek területére vonatkozó feltétel.
2. megoldás. Legyenek a háromszög szögei a szokásos módon \(\displaystyle \alpha,\beta,\gamma\), és legyen \(\displaystyle F'\) az \(\displaystyle F\) pont tükörképe az \(\displaystyle AOE\) szögfelezőre. A tükrözés miatt az \(\displaystyle AOF\) és \(\displaystyle AOF'\) háromszögek egybevágók és területük egyenlő. Mivel az \(\displaystyle ABO\) háromszög területe egyenlő az \(\displaystyle AOF\) és \(\displaystyle BEO\) háromszög területének összegével, a \(\displaystyle BOF'\) háromszög területe is megegyezik a \(\displaystyle BEO\) háromszög területével. Ennek a két háromszögnek tehát a területe megegyezik, a \(\displaystyle BO\) oldaluk közös, és a \(\displaystyle B\) csúcsnál ugyanakkora szögük van; ez csak úgy lehet, ha \(\displaystyle BE=BF'\), és a két háromszög egymás tükörképe a \(\displaystyle BOF\) szögfelezőre.
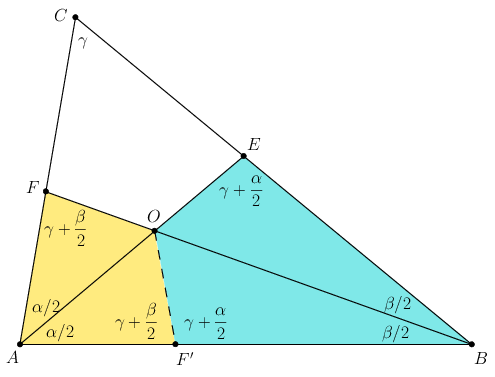
A \(\displaystyle BCF\) és \(\displaystyle AEC\) háromszögek szögeinek összeszámolásából látjuk, hogy
\(\displaystyle OF'A \sphericalangle = AFB\sphericalangle = FCB\sphericalangle + CBF\sphericalangle = \gamma+\frac\beta2 \)
és
\(\displaystyle BF'O \sphericalangle = AEB\sphericalangle = ACE\sphericalangle + EAC\sphericalangle = \gamma+\frac\alpha2. \)
Mivel \(\displaystyle OF'A \sphericalangle + BF'O \sphericalangle = 180^\circ\),
\(\displaystyle \left(\gamma+\frac\beta2\right) + \left(\gamma+\frac\alpha2\right) = 180^\circ \)
\(\displaystyle 2\gamma + \frac{\alpha+\beta}2 = 2\gamma + \frac{180^\circ-\gamma}2 = 180^\circ \)
\(\displaystyle \gamma = 60^\circ. \)
A megoldás teljességéhez hozzá tartozik annak ellenőrzése, hogy létezik a feladat feltételeinek megfelelő \(\displaystyle ABC\) háromszög, tehát az \(\displaystyle \gamma = 60^\circ\) valóban lehetséges.
Vegyük észre, hogy a lépéseink megfordíthatóak: ha a háromszögben \(\displaystyle \gamma=60^\circ\), akkor \(\displaystyle \left(\gamma+\frac\beta2\right) + \left(\gamma+\frac\alpha2\right) = 180^\circ\), így a \(\displaystyle BEO\) és \(\displaystyle BF'O\) háromszögek egybevágóak és egymás tükörképei, emiatt az \(\displaystyle ABO\) háromszög területe megegyezik az \(\displaystyle AOF\) és \(\displaystyle BEO\) háromszögek területösszegével.
Statistics:
109 students sent a solution. 3 points: 71 students. 2 points: 15 students. 1 point: 10 students. 0 point: 13 students.
Problems in Mathematics of KöMaL, January 2018
