Problem B. 4926. (January 2018)

B. 4926. In an acute-angled triangle \(\displaystyle ABC\), the feet of the altitudes drawn from \(\displaystyle B\) and from \(\displaystyle C\) are \(\displaystyle D\) and \(\displaystyle E\), respectively. The reflections of point \(\displaystyle E\) in the lines \(\displaystyle AC\) and \(\displaystyle BC\) are \(\displaystyle S\) and \(\displaystyle T\), respectively. The circle \(\displaystyle CST\), centred at \(\displaystyle O\), intersects line \(\displaystyle AC\) again at point \(\displaystyle X\ne C\). Show that lines \(\displaystyle XO\) and \(\displaystyle DE\) are perpendicular.

(Korean problem)

(5 pont)

Deadline expired on February 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle M\) a \(\displaystyle DE\) és \(\displaystyle OX\) egyenesek metszéspontja. Azt kell igazolnunk, hogy \(\displaystyle DMX\sphericalangle=90^\circ\). Ehhez a \(\displaystyle DMX\) háromszög másik két szögének összegét fogjuk kiszámítani.

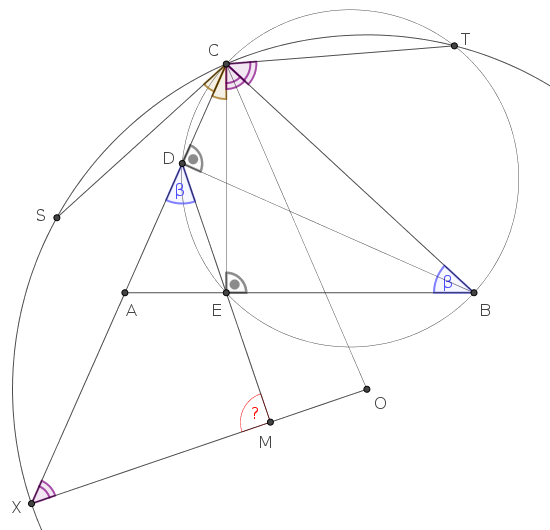
Legyen \(\displaystyle \beta=CBA\sphericalangle\). A \(\displaystyle D,E\) pontok a magasságok talppontjai, a \(\displaystyle BC\) szakasz Thalész-körén vannak, így

\(\displaystyle XDM\sphericalangle = 180^\circ-EDC\sphericalangle = CBA\sphericalangle = \beta. \)

Az \(\displaystyle OCX\) háromszögben \(\displaystyle OX=OC\) a \(\displaystyle CSTX\) kör sugarai, ezért \(\displaystyle OXC\sphericalangle = XCO\sphericalangle\). Az \(\displaystyle S\) és \(\displaystyle T\) pontok az \(\displaystyle E\) pont tükörképei, ezért a \(\displaystyle CAX\) egyenes felezi az \(\displaystyle SCE\), a \(\displaystyle CB\) egyenes pedig felezi az \(\displaystyle ECT\) szöget; továbbá \(\displaystyle CS=CE=CT\), így a \(\displaystyle CST\) körben az \(\displaystyle OC\) sugár felezi az \(\displaystyle SCT\) szöget. Végül az \(\displaystyle BCE\) derékszögű háromszögben \(\displaystyle ECB\sphericalangle=90^\circ-CBE\sphericalangle=90^\circ-\beta\). Mindezeket figyelembe véve

\(\displaystyle MXD\sphericalangle = OXC\sphericalangle = XCO\sphericalangle = SCO\sphericalangle - SCX\sphericalangle = \frac12 SCT\sphericalangle - \frac12 SCE\sphericalangle = \)

\(\displaystyle = \frac12 (SCT\sphericalangle - SCE\sphericalangle) = \frac12 ECT\sphericalangle = ECB\sphericalangle = 90^\circ-\beta. \)

A \(\displaystyle DXM\) háromszögben \(\displaystyle XDM\sphericalangle=\beta\) és \(\displaystyle MXD\sphericalangle=90^\circ-\beta\), tehát valóban \(\displaystyle DMX\sphericalangle=90^\circ\).

Megjegyzés. Érdemes megrajzolni az \(\displaystyle A\)-ból induló magasság talpponját (az ábrán \(\displaystyle F\)), és a \(\displaystyle BC\) egyenes másik, \(\displaystyle C\)-től különböző metszéspontját a \(\displaystyle CST\) körrel (\(\displaystyle Y\)). Jól ismert, hogy az \(\displaystyle F,D,S,T\) pontok egy egyenesre esnek, mert például \(\displaystyle SDA\sphericalangle = ADE\sphericalangle = CBA\sphericalangle = FDC\sphericalangle\), és ugyanígy \(\displaystyle BFT\sphericalangle=CFD\sphericalangle\). A \(\displaystyle T,E,X\) pontok, valamint ugyanígy az \(\displaystyle S,E,Y\) pontok is egy egyenesre esnek, mert \(\displaystyle STE\sphericalangle = DTE\sphericalangle = DCE\sphericalangle = SCX\sphericalangle = STX\sphericalangle\). Mivel \(\displaystyle SYX\sphericalangle = SCX\sphericalangle = SEA\sphericalangle\), az \(\displaystyle XY\) szakasz párhuzamos az \(\displaystyle AB\) oldallal.

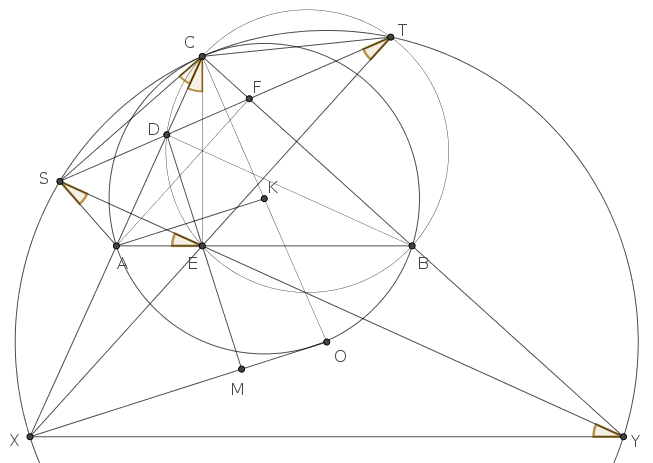
Az \(\displaystyle AXY\) háromszög tehát középpontosan hasonló az \(\displaystyle ABC\) háromszöghöz. Az \(\displaystyle ABC\) háromszög köré írt kör középpontját \(\displaystyle K\)-val jelölve, \(\displaystyle AK\|XO\), és a feladat állítása ekvivalens azzal a jól ismert ténnyel, hogy \(\displaystyle AK\perp DE\).

Statistics:

60 students sent a solution.
5 points:	55 students.
4 points:	1 student.
3 points:	2 students.
2 points:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, January 2018