Problem B. 4935. (February 2018)

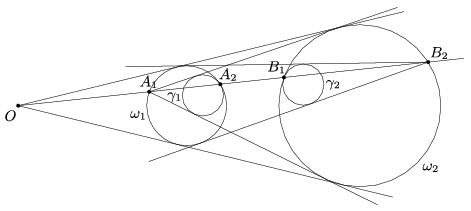
B. 4935. The given circles \(\displaystyle \omega_1\) and \(\displaystyle \omega_2\) lie inside an angle of vertex \(\displaystyle O\), touching the arms. A ray drawn from point \(\displaystyle O\) intersects circle \(\displaystyle \omega_1\) at points \(\displaystyle A_1\) and \(\displaystyle B_1\), and circle \(\displaystyle \omega_2\) at points \(\displaystyle A_2\) and \(\displaystyle B_2\), such that \(\displaystyle OA_1<OB_1<OA_2<OB_2\) (see the diagram). Circle \(\displaystyle \gamma_1\) touches the circle \(\displaystyle \omega_1\) on the inside, and also touches the tangents drawn to circle \(\displaystyle \omega_2\) from point \(\displaystyle A_1\). Similarly, circle \(\displaystyle \gamma_2\) touches the circle \(\displaystyle \omega_2\) on the inside, and also touches the tangents drawn to circle \(\displaystyle \omega_1\) from point \(\displaystyle B_2\). Prove that the radii of the circles \(\displaystyle \gamma_1\) and \(\displaystyle \gamma_2\) are equal.

(Kvant)

(5 pont)

Deadline expired on March 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tetszőleges \(\displaystyle c\) körre jelöljük \(\displaystyle r(c)\)-vel a \(\displaystyle c\) sugarát; azt kell igazolnunk, hogy \(\displaystyle r(\gamma_1)=r(\gamma_2)\). Jelöljük \(\displaystyle e\)-vel az \(\displaystyle OA_1A_2B_1B_2\) egyenest.

Az \(\displaystyle O\) pont a \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök közös külső érintőinek metszéspontja, tehát a két kör külső hasonlósági pontja; legyen \(\displaystyle \varphi_O\) az az \(\displaystyle O\) középpontú nagyítás, amelyre \(\displaystyle \varphi_O(\omega_1)=\omega_2\). Az \(\displaystyle e\) egyenes átmegy a nagyítás középpontján, ezért \(\displaystyle \varphi_0(e)=e\). Az \(\displaystyle A_1\) és az \(\displaystyle A_2\) pont az \(\displaystyle \omega_1\) kör és az \(\displaystyle e\) egyenes \(\displaystyle O\)-hoz közelebbi, illetve távolabbi metszéspontja, ezek képei az \(\displaystyle \omega_2\) kör és az \(\displaystyle e\) egyenes \(\displaystyle O\)-hoz közelebbi, illetve távolabbi metszéspontja: \(\displaystyle \varphi_0(A_1)=B_1\), illetve \(\displaystyle \varphi_0(A_2)=B_2\). A nagyítás aránya

\(\displaystyle \frac{r(\omega_2)}{r(\omega_1)}=\frac{B_1B_2}{A_1A_2}. \tag1 \)

Hasonlóan, a \(\displaystyle \gamma_1\) kört egy \(\displaystyle A_1\) középpontú \(\displaystyle \varphi_1\) nagyítás viszi át a \(\displaystyle \omega_2\) körbe úgy, hogy \(\displaystyle \varphi_1(A_2)=B_2\). Ennek a nagyításnak az aránya

\(\displaystyle \frac{r(\omega_2)}{r(\gamma_1)}=\frac{A_1B_2}{A_1A_2}. \tag2 \)

Végül, a \(\displaystyle \gamma_2\) kör is átvhető az \(\displaystyle \omega_1\) körbe egy \(\displaystyle B_2\) középpontú \(\displaystyle \varphi_2\) nagyítással úgy, hogy \(\displaystyle \varphi_2(B_1)=A_1\). Ennek a nagyításnak az aránya pedig

\(\displaystyle \frac{r(\omega_1)}{r(\gamma_2)}=\frac{A_1B_2}{B_1B_2}. \tag3 \)

Ha összeszorozzuk (1)-et, (3)-at és (2) reciprokát, azt kapjuk, hogy

\(\displaystyle \frac{r(\gamma_1)}{r(\gamma_2)} = \frac{r(\omega_2)}{r(\omega_1)} \cdot \frac{r(\omega_1)}{r(\gamma_2)} \cdot \frac{r(\gamma_1)}{r(\omega_2)} = \frac{B_1B_2}{A_1A_2} \cdot \frac{A_1B_2}{B_1B_2} \cdot \frac{A_1A_2}{A_1B_2} = 1, \)

vagyis valóban \(\displaystyle r(\gamma_1)=r(\gamma_2)\).

Statistics:

34 students sent a solution.
5 points:	Baski Bence, Beke Csongor, Busa 423 Máté, Csépányi István, Dobák Dániel, Döbröntei Dávid Bence, Fekete Richárd, Fuisz Gábor, Fülöp Anna Tácia, Gáspár Attila, Győrffi Ádám György, Győrffy Johanna, Hervay Bence, Jánosik Áron, Janzer Orsolya Lili, Kántor András Imre, Kerekes Anna, Nagy Nándor, Nguyen Bich Diep, Olosz Adél, Pituk Gábor, Póta Balázs, Schifferer András, Schrettner Jakab, Sebestyén Pál Botond, Soós 314 Máté, Szabó 417 Dávid, Szécsényi Nándor, Tiderenczl Dániel, Weisz Máté, Zsigri Bálint.
4 points:	Hegedűs Dániel.
2 points:	1 student.
1 point:	1 student.

Problems in Mathematics of KöMaL, February 2018