Problem B. 4936. (February 2018)

B. 4936. Let \(\displaystyle AB\) be a fixed chord that is not a diameter in a circle \(\displaystyle k\). The midpoint of \(\displaystyle AB\) is \(\displaystyle F\). Let \(\displaystyle P\) be a point on the circle \(\displaystyle k\), different from \(\displaystyle A\) and \(\displaystyle B\). Let the line \(\displaystyle PF\) intersect circle \(\displaystyle k\) again at \(\displaystyle X\), and let \(\displaystyle Y\) be the reflection of \(\displaystyle X\) in the perpendicular bisector of \(\displaystyle AB\). Prove that there exists a point in the plane that lies on the line \(\displaystyle PY\) for all \(\displaystyle P\).

Proposed by L. Surányi, Budapest

(5 pont)

Deadline expired on March 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Legyen a \(\displaystyle k\)-hoz \(\displaystyle A\)-ban és \(\displaystyle B\)-ben húzott érintők metszéspontja \(\displaystyle H\). Azt fogjuk megmutatni, hogy a \(\displaystyle PY\) egyenes átmegy a \(\displaystyle H\) ponton.

Legyen \(\displaystyle k\) középpontja \(\displaystyle O\), az \(\displaystyle AB\) húr felező merőlegese \(\displaystyle f\), ami átmegy az \(\displaystyle O\) és \(\displaystyle H\) pontokon. Az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepe felcserélhető, ezért feltehetjük, hogy \(\displaystyle P\) az \(\displaystyle f\)-nek az \(\displaystyle A\) pontot tartalmazó oldalán van.

1. eset: \(\displaystyle P\) a \(\displaystyle k\) kör és \(\displaystyle f\) egyik metszéspontja. Ekkor \(\displaystyle X=Y\) a másik metszéspont, így a \(\displaystyle PY\) egyenes éppen \(\displaystyle f\).

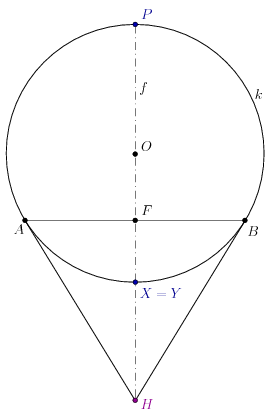
2. eset: A \(\displaystyle P\) pont a \(\displaystyle k\) kör hosszabbik \(\displaystyle AB\) ívén van, és \(\displaystyle AP<BP\).

Az \(\displaystyle AB\) és \(\displaystyle XY\) szakaszok párhuzamosak, mert mindkettő merőleges \(\displaystyle f\)-re. \(\displaystyle PXY\sphericalangle = PFA\sphericalangle = XFB\sphericalangle =AFY\sphericalangle\) miatt \(\displaystyle PFY\sphericalangle=2\cdot PXY\sphericalangle\). A kerületi és középponti szögek tétele miatt pedig \(\displaystyle POY\sphericalangle=2\cdot PXY\sphericalangle\). Tehát \(\displaystyle PFY\sphericalangle=POY\sphericalangle\), a kerületi szögek tételének megfordítása szerint a \(\displaystyle P,Y,Z,O\) pontok egy körön vannak.

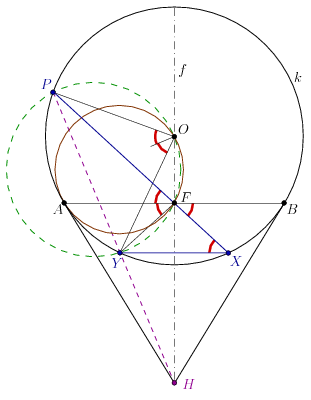
Rajzoljuk meg az \(\displaystyle AFO\) kört is, ami \(\displaystyle OFA\sphericalangle=90^\circ\) miatt az \(\displaystyle OA\) szakasz Thalész-köre. Az \(\displaystyle OA\) szakasz a \(\displaystyle k\) körnek sugara, az \(\displaystyle AFO\) körnek átmérője, ezért a két kör az \(\displaystyle A\) pontban érinti egymást; az \(\displaystyle AH\) egyenes a két kör közös érintője.

A \(\displaystyle PYFO\) kör, az \(\displaystyle AFO\) kör és \(\displaystyle k\) páronként vett hatványvonalai az \(\displaystyle AH\), \(\displaystyle f\) és \(\displaystyle PY\) egyenesek; ezek egy ponton, a három kör hatványpontján mennek át. Tehát a \(\displaystyle PY\) egyenes átmegy a \(\displaystyle H\) ponton.

3. eset: A \(\displaystyle P\) pont a \(\displaystyle k\) kör rövidebbik \(\displaystyle AB\) ívén van, és \(\displaystyle AP<BP\).

A 2. esethez hasonlóan, \(\displaystyle AFP\sphericalangle = YXF\sphericalangle = FYX\sphericalangle = YFA\sphericalangle\) miatt \(\displaystyle YFP\sphericalangle = 2\cdot YXP\sphericalangle = YOP\sphericalangle\), és így a \(\displaystyle P,F,O,Y\) pontok most is egy körön vannak.

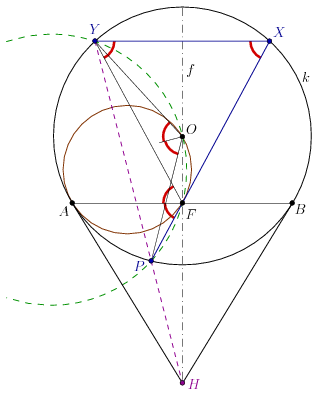
Az \(\displaystyle YPFO\) kör, az \(\displaystyle AFO\) kör és \(\displaystyle k\) páronként vett hatványvonalai az \(\displaystyle AH\), \(\displaystyle f\) és \(\displaystyle PY\) egyenesek, ezért a \(\displaystyle PY\) egyenes átmegy a \(\displaystyle H\) ponton, a másik két hatványvonal metszéspontján.

Megjegyzések. 1. Ha a \(\displaystyle P\) ponttal közelítünk az \(\displaystyle A\) vagy a \(\displaystyle B\) ponthoz, az \(\displaystyle Y\) pont is közeledni fog \(\displaystyle A\)-hoz, illetve \(\displaystyle B\)-hez. A \(\displaystyle PY\) egyenes két határhelyzete a \(\displaystyle K\)-hoz \(\displaystyle A\)-ban, illetve \(\displaystyle B\)-ben húzott érintők. Ez mutatja, hogy a lehetséges \(\displaystyle PY\) egyenesek közös pontja csak a \(\displaystyle H\) pont lehet.

2. Jól ismert a következő projektív geometriai tény: Ha a \(\displaystyle P,Q,X,H\) pontok a \(\displaystyle k\) körön fekszenek, akkor az \(\displaystyle I=PQ\cap XY\), \(\displaystyle F=PX\cap QY\) és \(\displaystyle H=PY\cap QX\) pontok mindegyike a másik két pont által meghatározott egyenes \(\displaystyle k\)-re vonatkozó pólusa. Speciálisan, a \(\displaystyle H\) pont az \(\displaystyle FI\) egyenes \(\displaystyle k\)-re vonatkozó pólusa (és az \(\displaystyle FI\) egyenes a \(\displaystyle H\) pont polárisa). Ha \(\displaystyle H\) a körön kívül helyezkedik el, és az \(\displaystyle FI\) egyenes a kört az \(\displaystyle A\) és \(\displaystyle B\) pontokban metszi, akkor \(\displaystyle HA\) és \(\displaystyle HB\) a \(\displaystyle H\)-ból \(\displaystyle k\)-hoz húzott érintők.

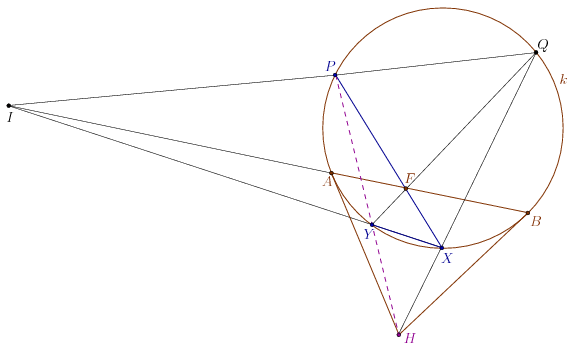
A megoldás alapjául szolgáló észrevétel, hogy a \(\displaystyle PY\) egyenes átmegy \(\displaystyle H\)-n, valójában a fenti tény egy határesete: ha \(\displaystyle PQ\|XY\), akkor \(\displaystyle I\) a két egyenes ideális pontja, és \(\displaystyle F\) az \(\displaystyle AB\) szakasz felezőpontja.

A körre vonatkozó polaritásról bővebben olvashatunk például a következő cikkekben:

    Kiss György: A körre vonatkozó polaritás. KöMaL, 1998. november, 450–455.

    Sz. C. Havalampijev: Pólus és poláris körben. KöMaL, 1987. január, 9–15.

2. megoldás. Az egységsugarúnak tekintett \(\displaystyle k\) kört úgy helyezzük el, hogy középpontja az origó, \(\displaystyle A\), \(\displaystyle B\) illetve \(\displaystyle F\) koordinátái rendre \(\displaystyle (-\cos\beta;\sin\beta)\), \(\displaystyle (\cos\beta;\sin\beta)\) és \(\displaystyle (0;\sin\beta)\). Jelölje \(\displaystyle P\), illetve \(\displaystyle X\) és \(\displaystyle Y\) koordinátáit rendre \(\displaystyle (x;y)\), \(\displaystyle (\cos y;\sin y)\) és \(\displaystyle (-\cos y;\sin y)\). Ekkor \(\displaystyle \sin \beta \neq 0\) és feltehető, hogy \(\displaystyle \cos x\neq 0\neq \cos y\), valamint \(\displaystyle \cos x \pm \cos y\neq 0\).

Mivel \(\displaystyle P\), \(\displaystyle F\) és \(\displaystyle X\) kollineárisak, azért

\(\displaystyle \frac{\sin x -\sin\beta}{\cos x}=\frac{\sin\beta - \sin y}{-\cos y}, \)

\(\displaystyle -\sin x\cos y+\sin\beta\cos y = \sin\beta\cos x - \cos x\sin y, \)

\(\displaystyle \sin (y-x) = \sin\beta (\cos x - \cos y). \)

Jelölje \(\displaystyle E\) a \(\displaystyle (0;\dfrac{1}{\sin\beta})\) koordinátájú pontot. (Ez éppen a kört \(\displaystyle A\)-ban és \(\displaystyle B\)-ben érintő egyenesek metszéspontja.) Megmutatjuk, hogy \(\displaystyle E\) a keresett pont. A \(\displaystyle P\), \(\displaystyle Y\) és \(\displaystyle E\) pontok ugyanis pontosan akkor kollineárisak, ha

\(\displaystyle \frac{\sin x - \sin y}{\cos x + \cos y} = \frac{\sin y - \frac{1}{\sin \beta}}{-\cos y}, \)

\(\displaystyle -\sin x\cos y + \sin y \cos y = \cos x \sin y + \sin y \cos y - \frac{1}{\sin \beta} (\cos x + \cos y), \)

\(\displaystyle \sin (x+y) = \frac{1}{\sin \beta} (\cos x + \cos y). \)

Ezzel ekvivalens feltételt kapunk, ha mindkét oldalt a nullától különböző \(\displaystyle 2\sin (y-x) = 2\sin\beta (\cos x - \cos y)\)-nal megszorozzuk:

\(\displaystyle 2\sin (x+y) \sin (y-x) = 2(\cos^2 x - \cos^2 y), \)

\(\displaystyle \cos((x+y)-(y-x)) - \cos((x+y)+(y-x)) = (2\cos^2 x - 1) - (2\cos^2 y- 1), \)

\(\displaystyle \cos 2x - \cos 2y = \cos 2x - \cos 2y, \)

ami valóban igaz.

Statistics:

48 students sent a solution.
5 points:	Argay Zsolt, Beke Csongor, Busa 423 Máté, Csépányi István, Csiszár Zoltán, Daróczi Sándor, Deák Bence, Döbröntei Dávid Bence, Fekete Richárd, Fitos Bence, Fuisz Gábor, Fülöp Anna Tácia, Füredi Erik Benjámin, Gáspár Attila, Geretovszky Anna, Győrffi Ádám György, Győrffy Ágoston, Hervay Bence, Jánosik Áron, Janzer Orsolya Lili, Kerekes Anna, Kószó Máté József, Kupás Vendel Péter, Márton Dénes, Mikulás Zsófia, Molnár-Sáska Zoltán, Nagy Nándor, Németh Ciprián, Pituk Gábor, Póta Balázs, Schifferer András, Schrettner Jakab, Sebestyén Pál Botond, Shuborno Das, Soós 314 Máté, Surján Anett, Szabó 417 Dávid, Szabó 997 Balázs István, Tiderenczl Dániel, Tóth Ábel, Tubak Dániel, Weisz Máté, Zsigri Bálint.
3 points:	1 student.
2 points:	2 students.
1 point:	2 students.

Problems in Mathematics of KöMaL, February 2018