Problem B. 4938. (February 2018)

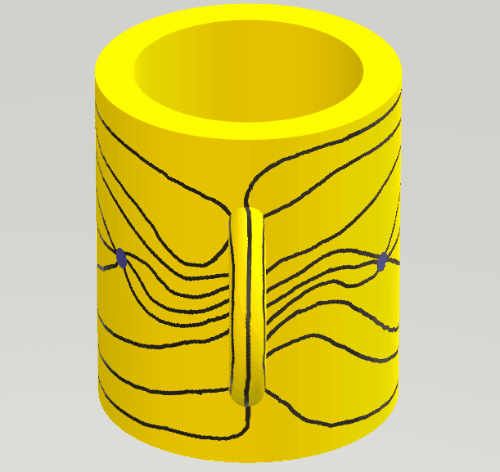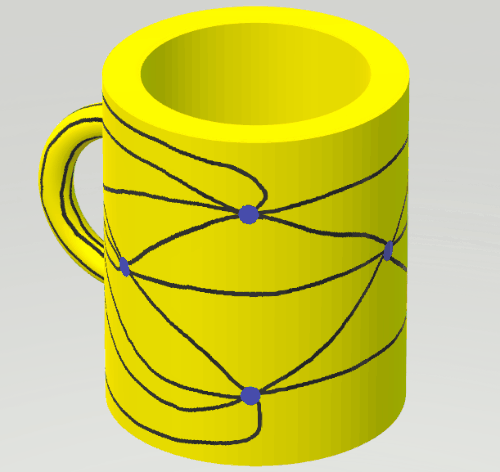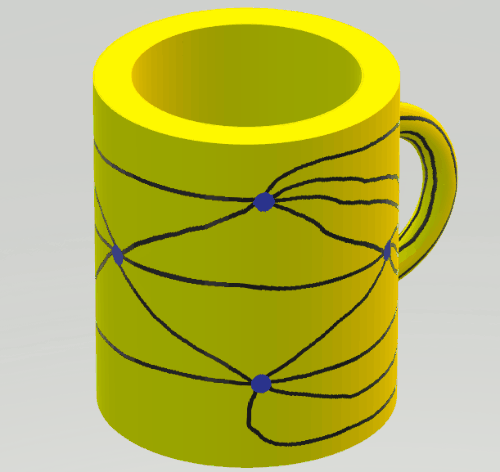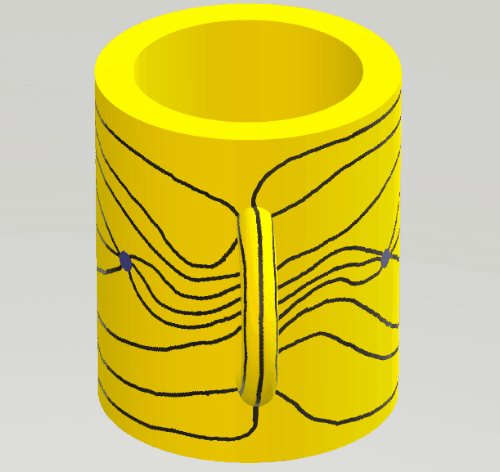
B. 4938. It is known that it is possible to draw the complete graph with \(\displaystyle 7\) vertices on the surface of a torus (see the Császár polyhedron, for example). 7 points are marked on the side of a mug. We want to connect each pair of points with a curve, so that the curves have no interior points in common. What minimum number of these curves need to lead across the handle of the mug?

(6 pont)

Deadline expired on March 12, 2018.

Solution (outline). In the first part we show that at least 6 edges must be lead through the handle; in the second part we provide a possible drawing of the graph in such a way that exactly 6 edges are drawn on the handle.

I. If we remove the handle from the mug and all curves on the handle, the body of the mug is homeomorphic with the sphere, so the 7 points with the remaining curves, considered as edges, form a planar graph. It is well-known that a planar graph with \(\displaystyle n\ge3\) vertices canot have more than \(\displaystyle 3n-6\) edges; our graph has \(\displaystyle n=7\) edges, so the number of remaining curves on the body of the mug is at most \(\displaystyle 3\cdot7-6=15\). The complete graph with 7 vertices has \(\displaystyle \binom72=21\) edges, so at least 6 edges must be lead through the handle.

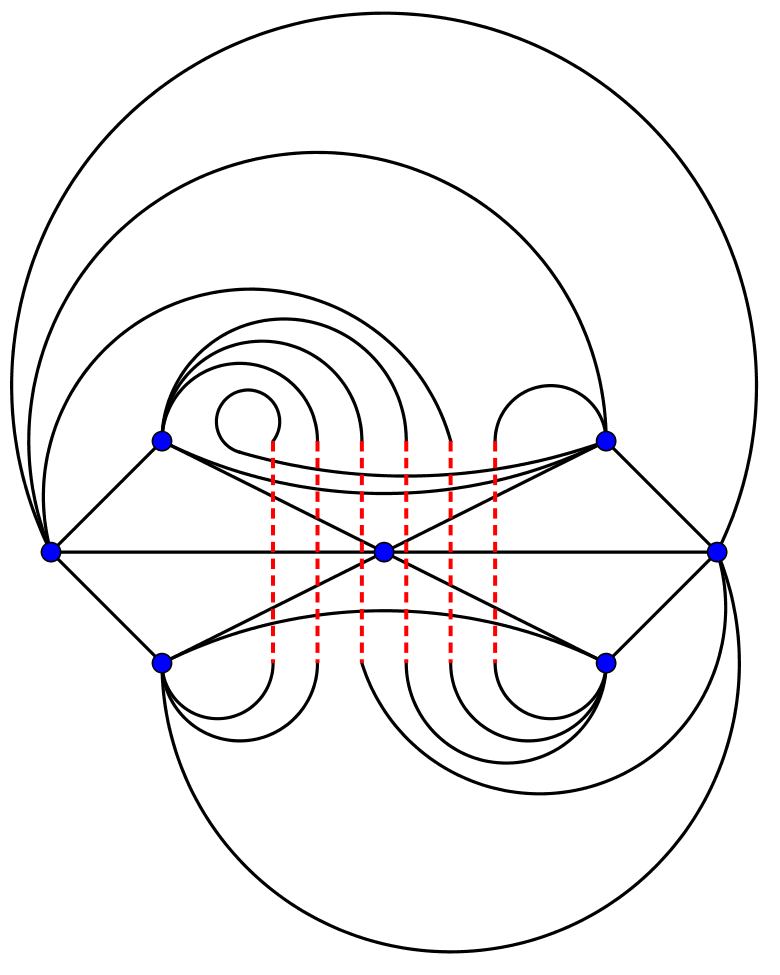
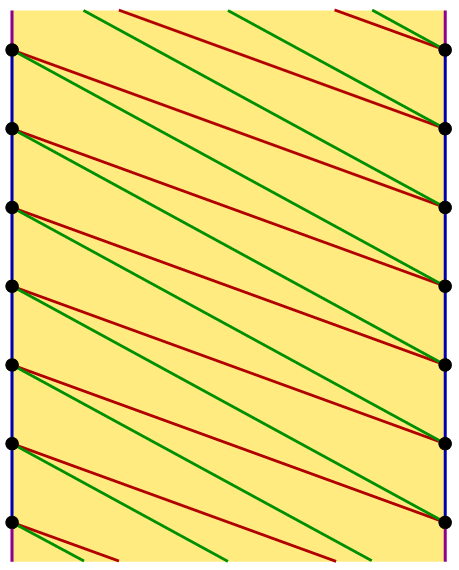
II. The left-hand picture shows a usual drawing of the complete graph with 7 vertices on the torus. Bonding the left and right-hand sides of the rectangle we obtain a pipe; bonding the two ends of the pipe (the upper and lower sides of the rectangle) through the handle we obtain a drawing of the graph, with exactly 6 edges on the handle, as shown in the right-hand picture.

Selected constructions from students' solutions

sent by Bence Hervay

sent by Máté Soós

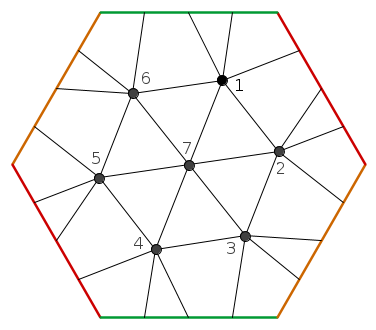
From the ideas of Gábor Pituk
(The opposite sides of the hexagon are bonded together; the handle is the closed curve formed by the red and the orange sides.)

sent by Attila Gáspár

Statistics:

30 students sent a solution.
6 points:	Döbröntei Dávid Bence, Gáspár Attila, Hegedűs Dániel, Hervay Bence, Kerekes Anna, Nagy Nándor, Schifferer András, Schrettner Jakab, Soós 314 Máté, Szabó 417 Dávid.
5 points:	Füredi Erik Benjámin.
4 points:	6 students.
3 points:	3 students.
2 points:	3 students.
0 point:	7 students.

Problems in Mathematics of KöMaL, February 2018