 |
A B. 4943. feladat (2018. március) |
B. 4943. Egy téglatest alakú tégla egyik lapjának mindegyik csúcsában van egy-egy hangya. A hangyák mindegyike a szemközti csúcshoz, azaz a saját csúcsához tartozó testátló másik végpontjába szeretne eljutni. Át tudnak-e menni a hangyák a tégla felszínén a szemközti csúcsba úgy, hogy az útvonalaik ne messék egymást és mind a négy hangya a lehető legrövidebb úton haladjon?
Javasolta: Gáspár Merse Előd (Budapest)
(4 pont)
A beküldési határidő 2018. április 10-én LEJÁRT.
Megoldás. Amíg egy hangya valamelyik lap síkjában halad, legrövidebb rész-útvonala egyenes szakasz; legrövidebb teljes útja ezért a téglatest egymáshoz csatlakozó lapjain haladó töröttvonal. Ha valamelyik csúcsból a három, azzal szomszédos lapok egyikén elindulva a lap határához ér, a megcélzott szemköztes csúcsot tartalmazó lapra jut, amelyen továbbmenve a kívánt csúcsba érkezik. A legrövidebb útvonal tehát két, a téglatest közös élben szomszédos lapján futó egy-egy szakaszból álló töröttvonal.
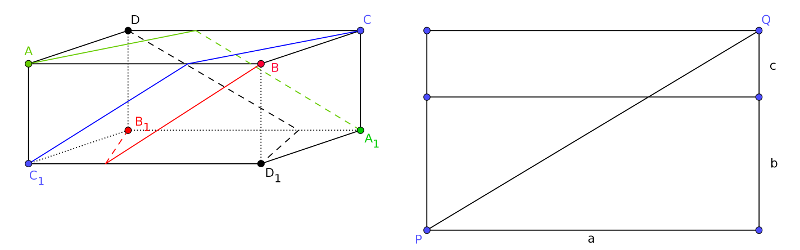
Terítsük ki egy síkba a legrövidebb utat tartalmazó két (szomszédos) lapot. Látható, hogy a \(\displaystyle P\) és \(\displaystyle Q\) pontok közötti legrövidebb út a \(\displaystyle PQ\) szakasz, amelynek hossza (az ábra jelöléseivel) \(\displaystyle \sqrt{a^2 + (b+c)^2}=\sqrt{a^2 + b^2 + c^2 + 2bc}\). Ez akkor minimális, ha \(\displaystyle a \geqslant b\,,\, c\). Tegyük fel, hogy az általános alakú téglatest élei közül \(\displaystyle AB\) a leghosszabb, és a hangyák kezdetben az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontokban tartózkodnak. Egymást nem metsző útvonalaikat az ábrán különböző színekkel megrajzolva láthatjuk.
Statisztika:
91 dolgozat érkezett. 4 pontot kapott: Baski Bence, Biczó Benedek, Bukva Dávid, Daróczi Sándor, Deák Bence, Dobák Dániel, Döbröntei Dávid Bence, Fekete Richárd, Fitos Bence, Füredi Erik Benjámin, Geretovszky Anna, Győrffy Ágoston, Győrffy Johanna, Hegedűs Dániel, Jánosik Áron, Kerekes Anna, Kovács 157 Zita, Mátravölgyi Bence, Nagy 551 Levente, Sebestyén Pál Botond, Shuborno Das, Soós 314 Máté, Surján Anett, Szőnyi Laura, Tiderenczl Dániel, Weisz Máté, Zsigri Bálint. 3 pontot kapott: Ács Andor, Apagyi Dávid, Barta Gergely, Csaplár Viktor, Gyetvai Miklós, Győrffi Ádám György, Hervay Bence, Jánosik Máté, Janzer Orsolya Lili, Kiss Gergely, Kószó Máté József, Kupás Vendel Péter, Mikulás Zsófia, Németh Ábel, Nguyen Bich Diep, Noszály Áron, Schrettner Jakab, Szabó 417 Dávid, Velich Nóra, Vida Tamás. 2 pontot kapott: 13 versenyző. 1 pontot kapott: 19 versenyző. 0 pontot kapott: 12 versenyző.
A KöMaL 2018. márciusi matematika feladatai

