 |
A B. 4944. feladat (2018. március) |
B. 4944. Jelölje \(\displaystyle t\) egy konvex \(\displaystyle \mathcal{S}\) síkidomba írt (valamely) maximális területű háromszög területét, míg \(\displaystyle T\) az \(\displaystyle \mathcal{S}\) köré írt (valamely) minimális területű háromszög területét. Mekkora a \(\displaystyle \frac{T}{t}\) hányados maximuma?
(5 pont)
A beküldési határidő 2018. április 10-én LEJÁRT.
Megoldás. Legyen \(\displaystyle ABC\) egy, az \(\displaystyle \mathcal{S}\) síkidomba írt (valamely) maximális területű háromszög (és így a területe: \(\displaystyle T_{ABC}=t\)).
Lemma: Megmutatjuk, hogy ekkor az az \(\displaystyle A'B'C'\) háromszög, aminek a középvonali háromszöge az \(\displaystyle ABC\) háromszög az \(\displaystyle \mathcal{S}\) síkidomot (belsejében és a határán) tartalmazó (nem feltétlenül minimális területű) háromszög.
Indirekt tegyük fel, hogy ez nem igaz, azaz az \(\displaystyle \mathcal{S}\) síkidomnak van olyan pontja, amelyet \(\displaystyle A'B'C'\) nem tartalmaz. Ekkor az \(\displaystyle A'B'C'\) háromszögnek legalább az egyik oldalegyenese két részre vágja az \(\displaystyle \mathcal{S}\) síkidomot. Legyen ez a metsző egyenes a \(\displaystyle B'C'\) oldalegyenes! Ekkor az \(\displaystyle \mathcal{S}\) határán van olyan \(\displaystyle A^*\) pont, amely a minimális \(\displaystyle t\) területű \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalától messzebb van, mint az \(\displaystyle A\) pont.
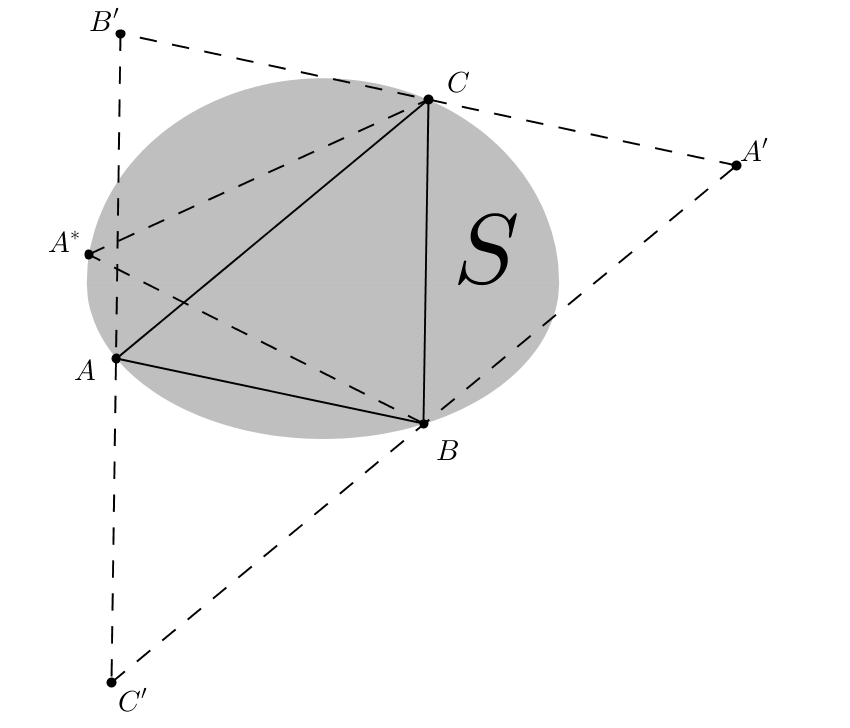
Viszont az \(\displaystyle \mathcal{S}\) síkidom konvexitása miatt ekkor az \(\displaystyle A^*BC\) háromszög teljesen \(\displaystyle \mathcal{S}\) belsejében van, másfelől viszont \(\displaystyle T_{A^*BC} > T_{ABC}=t\) (a \(\displaystyle BC\) oldalhoz tartozó magasságok miatt), ami ellentmond az \(\displaystyle ABC\) háromszög választásának.
Ezzel a lemmát igazoltuk.
A lemma alapján \(\displaystyle \dfrac{T}{t} \leq 4\). Viszont például az \(\displaystyle \mathcal{S}\)-t körnek választva triviálisan igaz az, hogy mind a megfelelő beírt, mind a megfelelő köréírt háromszögek olyan szabályos háromszögek, melyek területeinek az arányára éppen \(\displaystyle \dfrac{T}{t} = 4\).
Azaz a kérdéses arány maximuma: \(\displaystyle \boxed{\:\dfrac{T}{t} = 4. \:}\)
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Baski Bence, Beke Csongor, Csépányi István, Csiszár Zoltán, Dobák Dániel, Fekete Richárd, Fraknói Ádám, Füredi Erik Benjámin, Gáspár Attila, Győrffy Ágoston, Janzer Orsolya Lili, Kántor András Imre, Kerekes Anna, Kocsis Anett, Nagy Nándor, Pituk Gábor, Saár Patrik, Schrettner Jakab, Sebestyén Pál Botond, Soós 314 Máté, Surján Anett, Szabó 417 Dávid, Várkonyi Zsombor, Weisz Máté, Zólomy Kristóf, Zsigri Bálint. 3 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2018. márciusi matematika feladatai

