Problem B. 4958. (May 2018)

B. 4958. The sides of a triangle are \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), the radius of the inscribed circle is \(\displaystyle r\), and the radius of the circumscribed circle is \(\displaystyle R\). Prove that if

\(\displaystyle a+b+c =\frac{4}{rR} \quad\text{and}\quad \sqrt{ab}+\sqrt{bc}+\sqrt{ca} =6, \)

then \(\displaystyle R=2r\).

(Romanian competition problem)

(4 pont)

Deadline expired on June 11, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az 1. ábra jelöléseit. \(\displaystyle T_{ABC}=T_{ABK}+T_{BCK}+T_{ACK}=\frac{a+b+c}{2}\cdot r\), valamint \(\displaystyle T_{ABC}=\frac{ab\sin γ}{2}\).

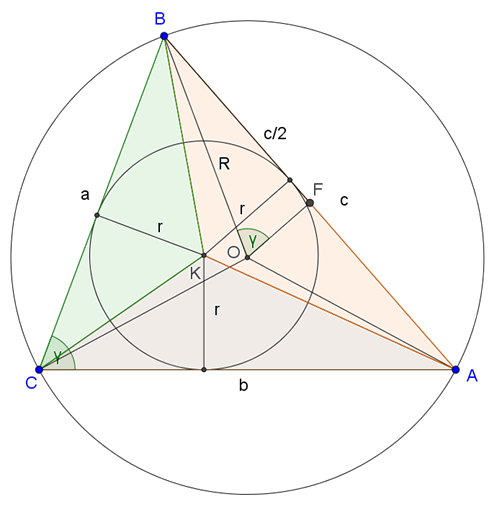
1. ábra

A \(\displaystyle BFO\) derékszögű háromszögben \(\displaystyle \frac c2=R\sin γ\). A feladat első egyenletéből:

\(\displaystyle \frac{a+b+c}{2}\cdot rR=2,\)

\(\displaystyle T_{ABC}\cdot R=2,\)

\(\displaystyle \frac{ab\sin γ}{2}\cdot R=2,\)

\(\displaystyle \frac{ab}{2}\cdot R\sin γ=2,\)

\(\displaystyle \frac{ab}{2}\cdot\frac c2=2,\)

\(\displaystyle abc=8.\)

Használjuk fel a számtani és mértani közép közötti összefüggést a második egyenlet jobb oldalának átalakítására:

\(\displaystyle \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{3}≥\root 3\of {\sqrt{ab}\sqrt{bc}\sqrt{ca}} =\root 3\of {abc},\)

\(\displaystyle 6=\sqrt{ab}+\sqrt{bc}+\sqrt{ca}≥3\root 3\of {abc}=3\root 3\of 8=6.\)

Ebből látszik, hogy a számtani és mértani közép egyenlő. Ez csak akkor lehetséges, ha \(\displaystyle a=b=c\), vagyis a háromszög egyenlő oldalú (2. ábra)

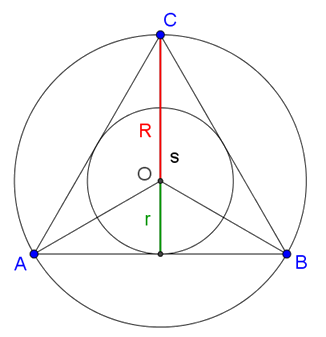
2. ábra

Ha egy egyenlő oldalú háromszögben s a súlyvonal hossza, akkor \(\displaystyle R=\frac23 s\), \(\displaystyle r=\frac13 s\), és így \(\displaystyle R=2r\).

Statistics:

68 students sent a solution.
4 points:	59 students.
3 points:	2 students.
2 points:	3 students.
1 point:	3 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, May 2018