Problem B. 4960. (May 2018)

B. 4960. Let \(\displaystyle P\) be an interior point of triangle \(\displaystyle ABC\), and let \(\displaystyle A^*\), \(\displaystyle B^*\) és \(\displaystyle C^*\) be arbitrary points of the line segments \(\displaystyle AP\), \(\displaystyle BP\) and \(\displaystyle CP\), respectively. Through point \(\displaystyle A^*\), draw parallels to \(\displaystyle BP\) and \(\displaystyle CP\), which intersect sides \(\displaystyle AB\) and \(\displaystyle AC\) at \(\displaystyle A_1\) and \(\displaystyle A_2\), respectively, as shown in the figure. Similarly, the parallels drawn through point \(\displaystyle B^*\) to \(\displaystyle CP\) and \(\displaystyle AP\) intersect sides \(\displaystyle BC\) and \(\displaystyle AB\) at \(\displaystyle B_1\) and \(\displaystyle B_2\), and finally, the parallels drawn through point \(\displaystyle C^*\) to \(\displaystyle AP\) and \(\displaystyle BP\) intersect sides \(\displaystyle AC\) and \(\displaystyle BC\) at \(\displaystyle C_1\) and \(\displaystyle C_2\), respectively. Show that

\(\displaystyle AC_1 \cdot BA_1 \cdot CB_1 = AB_2\cdot BC_2 \cdot CA_2. \)

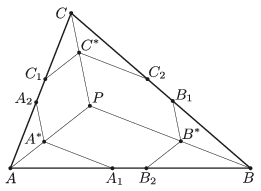
Proposed by J. Kozma, Szeged

(3 pont)

Deadline expired on June 11, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Írjuk fel a párhuzamos szelők tételét \(\displaystyle PAC\angle\)-ben \(\displaystyle A^*A_2\) és \(\displaystyle PC\) szelőkkel, így kapjuk, hogy

\(\displaystyle \frac{CA_2}{CA}=\frac{PA^*}{PA}.\)

Szintén a párhuzamos szelők tételét alkalmazva \(\displaystyle PAB\angle\)-ben \(\displaystyle A^*A_1\) és \(\displaystyle PB\) szelőkkel nyerjük, hogy:

\(\displaystyle \frac{PA^*}{PA}=\frac{BA_1}{BA}.\)

Így

\(\displaystyle \frac{CA_2}{CA}=\frac{BA_1}{BA}.\)

Hasonló megfontolásokkal beláthatjuk, hogy

\(\displaystyle \frac{AB_2}{AB}=\frac{PB^*}{PB}=\frac{CB_1}{CB} ;\quad \quad \frac{BC_2}{BC}=\frac{PC^*}{PC}=\frac{AC_1}{AC}.\)

A kapott három egyenlőség bal-, ill. jobboldalait összeszorozva

\(\displaystyle \frac{CA_2}{CA}\cdot \frac{AB_2}{AB}\cdot \frac{BC_2}{BC}=\frac{BA_1}{BA}\cdot \frac{CB_1}{CB} \cdot \frac{AC_1}{AC}\)

adódik, amiből az állítás következik.

Statistics:

60 students sent a solution.
3 points:	Al-Hag Máté Amin, Apagyi Dávid, Argay Zsolt, Baski Bence, Beke Csongor, Bukva Dávid, Bursics András, Daróczi Sándor, Deák Bence, Dobák Dániel, Döbröntei Dávid Bence, Fey Mihály, Fitos Bence, Fülöp Anna Tácia, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Győrffi Ádám György, Győrffy Johanna, Hervay Bence, Jánosik Áron, Kántor András Imre, Kerekes Anna, Kitschner Bernadett, Kocsis Anett, Kupás Vendel Péter, Mikulás Zsófia, Nguyen Bich Diep, Olosz Adél, Pituk Gábor, Póta Balázs, Reimann Kristóf, Sebestyén Pál Botond, Soós 314 Máté, Szabó 417 Dávid, Szabó 864 Blanka, Szőnyi Laura, Terjék András József, Tiderenczl Dániel, Tiszay Ádám, Tóth Ábel, Tubak Dániel, Velich Nóra.
2 points:	16 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, May 2018