Problem B. 4963. (May 2018)

B. 4963. Let \(\displaystyle r_a\) be the radius of the largest escribed circle of a triangle, and let \(\displaystyle R\) denote the radius of the circumscribed circle. Prove that \(\displaystyle r_a \ge \frac32 R\).

A problem from Paul Erdős (1913–1996)

(5 pont)

Deadline expired on June 11, 2018.

Soltuion 1. Let the sides of the triangle be \(\displaystyle a,b,c\), and let the semiperimeter be \(\displaystyle s=\frac{a+b+c}2\), let the aera by \(\displaystyle A\). As is well-known,

\(\displaystyle A = \frac{abc}{4R}; \quad A = r_a(s-a) = r_b(s-b) = r_c(s-c); \)

\(\displaystyle A^2 = s(s-a)(s-b)(s-c) \quad \text{(Héron's formula)}. \)

Hence,

\(\displaystyle R = \frac{abc}{4A} \)

and

\(\displaystyle r_a = \frac{A}{s-a} = \frac{t^2}{A(s-a)} = \frac{s(s-a)(s-b)(s-c)}{A(s-a)} = \frac{s(s-b)(s-c)}{A}. \)

By the condition, \(\displaystyle r_a\ge r_b\) and \(\displaystyle r_a\ge r_c\); equivalently \(\displaystyle s-a\le s-b\) and \(\displaystyle s-a\le s-c\). Choose \(\displaystyle s-a\) to be of unit length; let \(\displaystyle s-a=1\), \(\displaystyle s-b=1+x\) and \(\displaystyle s-c=1+y\) with some \(\displaystyle x,y\ge0\). Then \(\displaystyle a=(s-b)+(s-c)=2+x+y\), \(\displaystyle b=(s-a)+(s-c)=2+y\), \(\displaystyle c=(s-a)+(s-b)=2+x\), \(\displaystyle s=(s-a)+(s-b)+(s-c)=3+x+y\). Therefore,

\(\displaystyle r_a - \frac32 R = \frac{s(s-b)(s-c)}{A} - \frac{3abc}{8A} = \)

\(\displaystyle = \frac{8(3+x+y)(1+x)(1+y)-3(2+x+y)(2+y)(2+x)}{8A} = \)

\(\displaystyle = \frac{8x+8y+2x^2+22xy+2y^2+5x^2y+5xy^2}{8A} \ge 0, \)

so indeed \(\displaystyle r_a\ge\frac32R\). It can be seen that equality occurs only if \(\displaystyle x=y\), i.e. the triangle is equilateral.

Solution 2.. Let the vertices of the triangle be \(\displaystyle A,B,C\), let the circumcenter be \(\displaystyle O\), let the centers of the excircles be \(\displaystyle J_a,J_b,J_c\), let their radii be \(\displaystyle r_a,r_b,r_c\), and let \(\displaystyle d_a=OJ_a\), \(\displaystyle d_b=OJ_b\) and \(\displaystyle d_c=OJ_c\).

By Euler's formulae

\(\displaystyle d_a^2 = R(R+2r_a), \quad d_b^2 = R(R+2r_b), \quad d_c^2 = R(R+2r_c); \)

Therefore, it suffices to show \(\displaystyle d_a\ge 2R\).

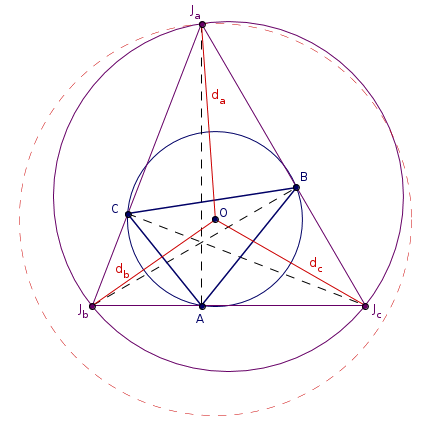
The triangle \(\displaystyle J_aJ_bJ_c\) is acute angled, its sides are the external angle bisectors of the triangle \(\displaystyle ABC\), the its altitudes are the angle bisectors. The 9-point circle of triangle \(\displaystyle J_aJ_bJ_c\) is the circle \(\displaystyle ABC\). The radius of the 9-point circle is half of the circumradius, so the radius of circle \(\displaystyle J_aJ_bJ_c\) is precisely \(\displaystyle 2R\).

The smallest circular disk that covers a acute angle is its circumcircle. The disk with center \(\displaystyle O\) and radius \(\displaystyle d_a\) covers the triangle \(\displaystyle J_aJ_bJ_c\), so \(\displaystyle d_a\ge 2R\).

Statistics:

39 students sent a solution.
5 points:	Baski Bence, Beke Csongor, Daróczi Sándor, Deák Bence, Dobák Dániel, Fitos Bence, Füredi Erik Benjámin, Gáspár Attila, Győrffi Ádám György, Győrffy Ágoston, Hegedűs Dániel, Jánosik Áron, Kerekes Anna, Pituk Gábor, Richlik Róbert, Schrettner Jakab, Szabó 417 Dávid, Szabó 991 Kornél, Tiderenczl Dániel, Tubak Dániel, Weisz Máté.
4 points:	Csiszár Zoltán, Döbröntei Dávid Bence, Fekete Richárd, Noszály Áron, Póta Balázs, Shuborno Das, Szabó 864 Blanka, Tóth Ábel.
3 points:	5 students.
2 points:	2 students.
1 point:	3 students.

Problems in Mathematics of KöMaL, May 2018