 |
A B. 4967. feladat (2018. szeptember) |
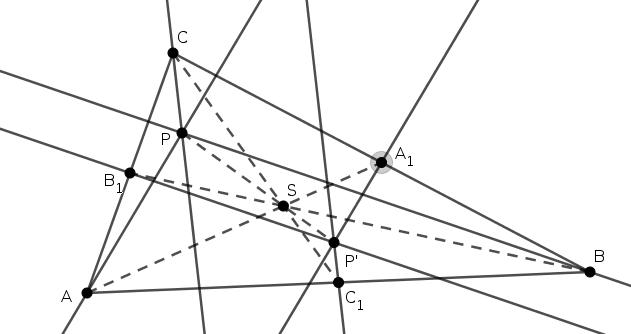
B. 4967. Az \(\displaystyle ABC\triangle\) belső pontja \(\displaystyle P\), az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle C_1\), a \(\displaystyle BC\) oldalé \(\displaystyle A_1\), a \(\displaystyle CA\) oldalé \(\displaystyle B_1\). Húzzunk párhuzamosokat rendre az \(\displaystyle AP\), \(\displaystyle BP\) és \(\displaystyle CP\) egyenesekkel az \(\displaystyle A_1\), \(\displaystyle B_1\), illetve \(\displaystyle C_1\) pontokon keresztül. Mutassuk meg, hogy ez a három egyenes egy pontban metszi egymást.
Javasolta: Kozma József (Szeged)
(3 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
Megoldás. Legyen az \(\displaystyle ABC\triangle\) súlypontja \(\displaystyle S\). Az \(\displaystyle S\) középpontú, \(\displaystyle \lambda=-1/2\) arányú középpontos hasonlóság az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) pontokat rendre az \(\displaystyle A_1\), \(\displaystyle B_1\), ill. \(\displaystyle C_1\) pontokba képezi a súlypont ismert tulajdonsága miatt. Legyen továbbá a \(\displaystyle P\) pont képe \(\displaystyle P'\). Így az \(\displaystyle AP\), \(\displaystyle BP\) és \(\displaystyle CP\) egyenesek képei rendre \(\displaystyle A_1P'\), \(\displaystyle B_1P'\) és \(\displaystyle C_1P'\); és így a középpontos hasonlóság ismert tulajdonsága miatt \(\displaystyle AP\parallel A_1P'\), \(\displaystyle BP\parallel B_1P'\), ill. \(\displaystyle CP\parallel C_1P'\). Kaptuk, hogy az \(\displaystyle A_1\)-re illeszkedő, \(\displaystyle AP\)-vel párhuzamos egyenes éppen \(\displaystyle A_1P'\), a \(\displaystyle B_1\)-re illeszkedő, \(\displaystyle BP\)-vel párhuzamos egyenes éppen \(\displaystyle B_1P'\) és a \(\displaystyle C_1\)-re illeszkedő, \(\displaystyle CP\)-vel párhuzamos egyenes éppen \(\displaystyle C_1P'\). Vagyis a szóban forgó egyenesek mindegyike illeszkedik a \(\displaystyle P'\) pontra, amivel a feladat állítását beláttuk.
Statisztika:
131 dolgozat érkezett. 3 pontot kapott: 112 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2018. szeptemberi matematika feladatai

