Problem B. 4969. (September 2018)

B. 4969. The sides of a rectangle \(\displaystyle T\) are \(\displaystyle a\le b\). Given that the union of two appropriate disks of radius \(\displaystyle r\) covers \(\displaystyle T\) but this is impossible with two disks of radii smaller than \(\displaystyle r\), determine the length \(\displaystyle r\).

(4 pont)

Deadline expired on October 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek \(\displaystyle AB=CD=b\) és \(\displaystyle BC=DA=a\), az \(\displaystyle AB\), \(\displaystyle CD\) és \(\displaystyle DA\) oldalak felezőpontjai pedig rendre \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle G\) (az ábra szerint).

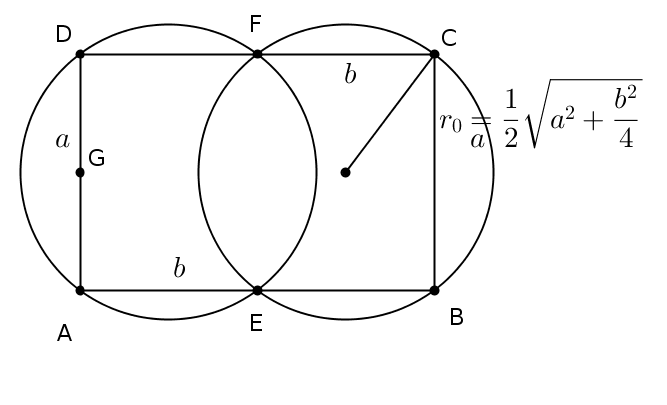
Az \(\displaystyle AEFD\) és \(\displaystyle FEBC\) téglalapok körülírt köreinek sugara (Pitagorasz tétele alapján) \(\displaystyle r_0 = \dfrac{1}{2} \sqrt{a^2+\dfrac{b^2}{4}}\). Ezek a körök együttesen lefedik \(\displaystyle ABCD\)-t, ezért \(\displaystyle 2r \leq \sqrt{a^2+\dfrac{b^2}{4}}=2r_0\).

Megmutatjuk, hogy szükségképpen \(\displaystyle r\geq r_0\) is teljesül. Tegyük fel, hogy valamely \(\displaystyle k_1\) és \(\displaystyle k_2\) \(\displaystyle r\) sugarú körök együttesen lefedik \(\displaystyle T\)-t. (Felhasználjuk, hogy \(\displaystyle k_1\) és \(\displaystyle k_2\) szerepe szimmetrikus.)

Ha \(\displaystyle k_1\) kör tartalmazza \(\displaystyle T\) három csúcsát, akkor két szemköztit is, így átmérője legalább \(\displaystyle 2r \geq \sqrt{a^2+b^2}>2r_0\).

Tegyük fel a továbbiakban, hogy \(\displaystyle k_1\) csak a \(\displaystyle T\) két szomszédos csúcsát tartalmazza, vagy \(\displaystyle A\)-t és \(\displaystyle B\)-t, vagy \(\displaystyle A\)-t és \(\displaystyle D\)-t.

1. eset. Ha \(\displaystyle k_1\) \(\displaystyle A\)-t és \(\displaystyle B\)-t (és így \(\displaystyle k_2\) \(\displaystyle C\)-t és \(\displaystyle D\)-t) tartalmazza, akkor valamelyik kör, mondjuk \(\displaystyle k_1\), tartalmazza \(\displaystyle G\)-t, ezért átmérője \(\displaystyle 2r\geq BG= \sqrt{b^2+\dfrac{a^2}{4}}\), amire (\(\displaystyle a\leq b\) miatt) \(\displaystyle 2r\geq \sqrt{b^2+\dfrac{a^2}{4}}\geq \sqrt{a^2+\dfrac{b^2}{4}}=2r_0\).

2. eset. Ha \(\displaystyle k_1\) csak az \(\displaystyle A\) és \(\displaystyle D\) (és így \(\displaystyle k_2\) \(\displaystyle B\) és \(\displaystyle C\)) csúcsokat tartalmazza, akkor valamelyik kör, mondjuk \(\displaystyle k_1\), tartalmazza \(\displaystyle E\)-t, ezért átmérője \(\displaystyle 2r\geq DE=\sqrt{a^2+\dfrac{b^2}{4}}=2r_0\).

Vagyis valóban azt kaptuk, hogy \(\displaystyle \boxed{\: r = \dfrac{1}{2} \sqrt{a^2+\dfrac{b^2}{4}} \:}\)  .

Statistics:

180 students sent a solution.
4 points:	51 students.
3 points:	11 students.
2 points:	21 students.
1 point:	75 students.
0 point:	18 students.
Not shown because of missing birth date or parental permission:	4 solutions.

Problems in Mathematics of KöMaL, September 2018