Problem B. 4970. (September 2018)

B. 4970. A line \(\displaystyle e\) in the plane separates two given points \(\displaystyle A\) and \(\displaystyle B\) of the plane. On the line \(\displaystyle e\), select points \(\displaystyle P\) and \(\displaystyle Q\) such that \(\displaystyle \angle PAQ=90^{\circ}\). Show that there exists a point different from \(\displaystyle B\) that lies on all circles drawn through \(\displaystyle B\), \(\displaystyle P\) and \(\displaystyle Q\), independently of the choice of \(\displaystyle P\) and \(\displaystyle Q\).

Proposed by the class 11C of Fazekas Primary and Secondary School, Budapest

(5 pont)

Deadline expired on October 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

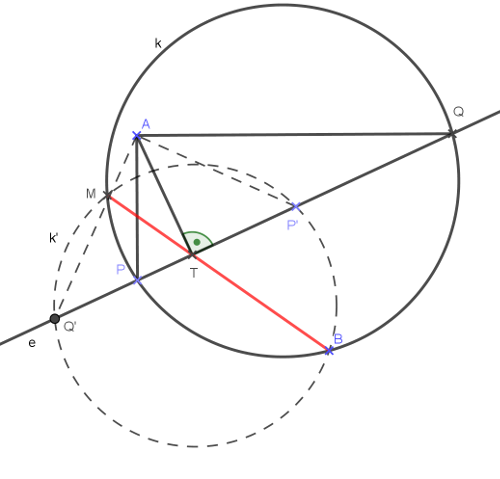
Legyen az \(\displaystyle APQ\) derékszögű háromszög átfogóhoz tartozó magasságának talppontja az \(\displaystyle e\) egyenesen a \(\displaystyle T\) pont. A magasságtétel alapján

\(\displaystyle PT \cdot TQ =AT^2.\)

Ez a szorzat a \(\displaystyle P\) és \(\displaystyle Q\) pontok összes lehetséges helyzetére ugyanez az \(\displaystyle AT^2\), vagyis állandó. Vegyünk most egy olyan \(\displaystyle k\) kört, amely átmegy a \(\displaystyle P, B\) és \(\displaystyle Q\) pontokon és hosszabbítsuk meg a \(\displaystyle TB\) szakaszt úgy, hogy messe még egy pontban, az \(\displaystyle M\) pontban a \(\displaystyle k\) kört. A \(\displaystyle k\) kör \(\displaystyle T\) pontra vonatkozó hatványa alapján

\(\displaystyle PT \cdot TQ=BT \cdot TM=AT^2=\text{áll}. \)

Az \(\displaystyle M\) pont helyzetét a rögzített \(\displaystyle A, T\) és \(\displaystyle B\) pontok egyértelműen meghatározák, ennek helyzete nem függ a \(\displaystyle P\) és \(\displaystyle Q\) megválasztásától. Az \(\displaystyle M\) pont mindegyik megfelelő \(\displaystyle k\) körön rajta van.

Statistics:

56 students sent a solution.
5 points:	Apagyi Dávid, Baski Bence, Beke Csongor, Bencsik Ádám, Bokor Endre, Bukva Dávid, Bursics András, Csertán András, Csiszár Zoltán, Deák Bence, Dobák Dániel, Espán Márton, Fajszi Bulcsú, Fekete Richárd, Fitos Bence, Fraknói Ádám, Fülöp Anna Tácia, Füredi Erik Benjámin, Győrffi Ádám György, Győrffy Ágoston, Győrffy Johanna, Hámori Janka, Hervay Bence, Hoffmann Balázs, Jedlovszky Pál, Keltai Dóra, Kerekes Anna, Kitschner Bernadett, Le Julianna Phuonglinh, Márton Dénes, Nagy Nándor, Nguyen Bich Diep, Noszály Áron, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Velich Nóra, Weisz Máté, Zsigri Bálint.
4 points:	Daniel Ghenghea.
3 points:	1 student.
2 points:	1 student.
1 point:	3 students.
0 point:	4 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, September 2018