 |
A B. 4972. feladat (2018. szeptember) |
B. 4972. Az \(\displaystyle ABC\) hegyesszögű háromszög belső \(\displaystyle P\) pontjának az oldalakra vett merőleges vetületei az ábra szerint \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Az oldalakon keletkező hat szakaszra kifelé négyzeteket rajzolunk, amiket felváltva két színnel színezünk az ábra szerint. Az azonos színű négyzetek ,,külső'' oldalegyenesei egy-egy háromszöget határoznak meg. Mutassuk meg, hogy ez a két háromszög egybevágó.
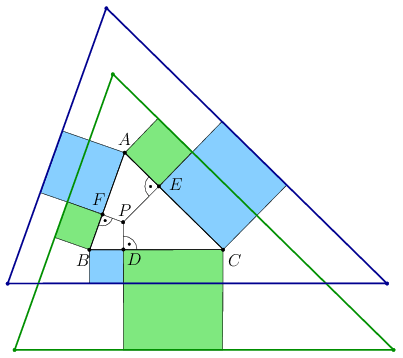
(6 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit.
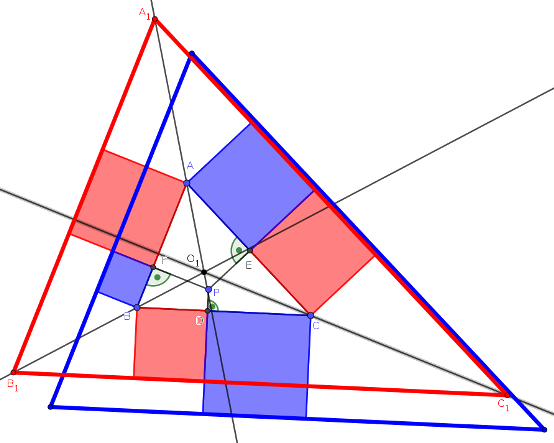
Először belátunk két segédállítást.
1. Segédállítás: \(\displaystyle BD^2+CE^2+AF^2=BF^2+AE^2+CD^2\), azaz a piros és kék négyzetek területei egyenlőek.
Bizonyítás. Felírhatjuk a Pitagorasz-tételt a \(\displaystyle BDP\), \(\displaystyle DCP\), \(\displaystyle CEP\), \(\displaystyle EAP\), \(\displaystyle AFP\) és \(\displaystyle FBP\) háromszögek mindegyikére. Ebből
\(\displaystyle BD^2+CE^2+AF^2=PB^2-PD^2+PC^2-PE^2+PA^2-PF^2=PB^2-PF^2+PC^2-PD^2+PA^2-PE^2=BF^2+AE^2+CD^2.\)
Ezzel az 1. segédállítást beláttuk.
2. Segédállítás: Létezik egy középpontos hasonlóság, amely az \(\displaystyle ABC\) háromszöget az \(\displaystyle A_1B_1C_1\) háromszögbe képezi.
Bizonyítás. Világos, hogy \(\displaystyle ABC\) és \(\displaystyle A_1B_1C_1\) oldalai páronként párhuzamosak, ezért szögeik páronként megegyeznek, így a két háromszög hasonló. Jelölje a hasonlóságuk arányát \(\displaystyle \lambda_1\). Legyen \(\displaystyle O_1\) az a pont, amelyre igaz, hogy az \(\displaystyle O_1\) középpontú, \(\displaystyle \lambda_1\) arányú hasonlóság az \(\displaystyle A\) pontot \(\displaystyle A_1\)-be képezi. A középpontos hasonlóság tulajdonságai miatt \(\displaystyle AB\) képe egy vele párhuzamos, \(\displaystyle \lambda_1\cdot AB\) hosszúságú szakasz lesz, amely így szükségképpen éppen \(\displaystyle A_1B_1\), azaz \(\displaystyle B\) képe \(\displaystyle B_1\). Ugyanígy \(\displaystyle C\) képe \(\displaystyle C_1\), és ezzel a 2. segédállítást is beláttuk.
Jelölje az \(\displaystyle O_1\) pont távolságát az \(\displaystyle ABC\) háromszög \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) oldalaitól rendre \(\displaystyle \hat a\), \(\displaystyle \hat b\) és \(\displaystyle \hat c\). A piros négyzetek oldalaira vezessük be az \(\displaystyle a_l=BD\), \(\displaystyle b_l=CE\) és \(\displaystyle c_l=AF\) jelöléseket. Világos, hogy ekkor az \(\displaystyle O_1\) pont távolsága az \(\displaystyle A_1B_1C_1\) háromszög oldalaitól rendre \(\displaystyle \hat a+a_l\), \(\displaystyle \hat b+b_l\) és \(\displaystyle \hat c+c_l\). A középpontos hasonlóság miatt \(\displaystyle \hat a\colon \hat b \colon \hat c= (\hat a+a_l)\colon (\hat b+b_l) \colon (\hat c +c_l)\), amiből viszont azonnal következik, hogy
\(\displaystyle \frac{a_l}{\hat a}=\frac{b_l}{\hat b}=\frac{c_l}{\hat c}=\lambda_1-1. \tag{1}\)
Most vegyük észre, hogy az \(\displaystyle ABO_1\), \(\displaystyle BCO_1\) és \(\displaystyle CAO_1\) háromszögek területeinek összege éppen az \(\displaystyle ABC\) háromszög \(\displaystyle T\) területével egyenlő, ebből
\(\displaystyle a\hat a+b\hat b+c \hat c=2T \tag{2}.\)
Továbbá, az 1. segédállítás szerint \(\displaystyle a_l^2+b_l^2+c_l^2=(a-a_l)^2+(b-b_l)^2+(c-c_l)^2\), amiből a négyzetreemelések elvégzése és rendezés után
\(\displaystyle aa_l+bb_l+cc_l=\frac{a^2+b^2+c^2}{2}.\)
Ebbe visszahelyettesítve (1)-et kapjuk, hogy
\(\displaystyle (\lambda_1-1)(a\hat a+b\hat b+c \hat c)=\frac{a^2+b^2+c^2}{2}.\tag{3}\)
A (2) és (3) összefüggéseket összevetve az \(\displaystyle A_1B_1C_1\) és \(\displaystyle ABC\) \(\displaystyle \lambda_1\) hasonlósági arányára
\(\displaystyle \lambda_1=\frac{a^2+b^2+c^2}{4T}+1.\)
Vegyük észre, hogy \(\displaystyle \lambda_1\) független \(\displaystyle P\) választásától. Hasonlóan kiszámolhatjuk a kék \(\displaystyle A_2B_2C_2\) és \(\displaystyle ABC\) háromszögek \(\displaystyle \lambda_2\) hasonlósági arányát is, és a \(\displaystyle \lambda_1=\lambda_2\) egyenlőség igazolja az állítást.
Statisztika:
46 dolgozat érkezett. 6 pontot kapott: Beke Csongor, Biczó Benedek, Bognár 171 András Károly, Bokor Endre, Bukva Dávid, Csaplár Viktor, Csiszár Zoltán, Dávid Levente, Deák Bence, Geretovszky Anna, Győrffy Ágoston, Hegedűs Dániel, Hoffmann Balázs, Jedlovszky Pál, Kerekes Anna, Kerekes Boldizsár, Kocsis Anett, Markó Gábor, Márton Dénes, Nagy Nándor, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Weisz Máté, Zsigri Bálint. 5 pontot kapott: Gyetvai Miklós, Hervay Bence, Stomfai Gergely. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2018. szeptemberi matematika feladatai

