 |
A B. 4979. feladat (2018. október) |
B. 4979. Az \(\displaystyle ABC\) hegyesszögű háromszögben \(\displaystyle D\) és \(\displaystyle E\) rendre az \(\displaystyle AB\), illetve az \(\displaystyle AC\) oldalnak belső pontja. A \(\displaystyle BE\) és \(\displaystyle CD\) szakaszok metszéspontja \(\displaystyle F\). Bizonyítsuk be, hogy ha \(\displaystyle BC^2=BD\cdot BA+CE\cdot CA\), akkor \(\displaystyle ADFE\) húrnégyszög.
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. Vegyük észre, hogy a \(\displaystyle BC\) oldal bármely \(\displaystyle M\) belső pontjára
\(\displaystyle BC\cdot BM + CB\cdot CM = BC\cdot(BM+MC) = BC^2 = BD\cdot BA+CE\cdot CA. \)
Válasszuk meg az \(\displaystyle M\) pontot úgy, hogy \(\displaystyle BC\cdot BM=BD\cdot BA\) legyen, ekkor az is automatikusan teljesülni fog, hogy \(\displaystyle CB\cdot CM = CE\cdot CA\). (Mivel \(\displaystyle BM=\frac{BC\cdot BM}{BC} < \frac{BC^2}{BC} = BC\), az \(\displaystyle M\) biztosan belső pontja a \(\displaystyle BC\) szakasznak.)
A szelőtétel megfordítása szerint a \(\displaystyle BC\cdot BM=BD\cdot BA\) és \(\displaystyle CB\cdot CM = CE\cdot CA\) egyenlőségekből következik, hogy \(\displaystyle ABME\) és \(\displaystyle ADMC\) húrnégyszögek.
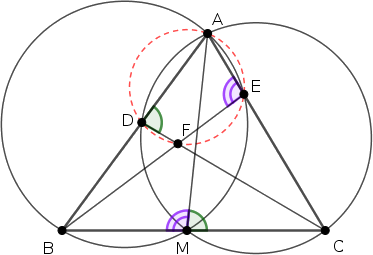
Ezek után az \(\displaystyle ADFE\) négyszög szemközti szögeinek összege
\(\displaystyle ADF\sphericalangle+FEA\sphericalangle = AMC\sphericalangle+BMA\sphericalangle = 180^\circ,\)
ezért az \(\displaystyle ADFE\) valóban húrnégyszög.
Statisztika:
36 dolgozat érkezett. 5 pontot kapott: Baski Bence, Beke Csongor, Csaplár Viktor, Dobák Dániel, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Győrffy Ágoston, Hegedűs Dániel, Hervay Bence, Hoffmann Balázs, Jánosik Áron, Kerekes Anna, Kerekes Boldizsár, Kiss 014 Dávid, Kocsis Anett, Kovács 129 Tamás, Markó Gábor, Márton Dénes, Mátravölgyi Bence, Nguyen Bich Diep, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Weisz Máté. 4 pontot kapott: Nguyễn Minh Khang, Szabó 991 Kornél. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2018. októberi matematika feladatai

