Problem B. 4979. (October 2018)

B. 4979. In an acute angled triangle \(\displaystyle ABC\), \(\displaystyle D\) and \(\displaystyle E\) are interior points of the sides \(\displaystyle AB\) and \(\displaystyle AC\), respectively. The line segments \(\displaystyle BE\) and \(\displaystyle CD\) meet at \(\displaystyle F\). Prove that if \(\displaystyle BC^2=BD\cdot BA+CE\cdot CA\) then the quadrilateral \(\displaystyle ADFE\) is cyclic.

Proposed by S. Róka, Nyíregyháza

(5 pont)

Deadline expired on November 12, 2018.

Solution. Notice that for any interior point \(\displaystyle M\) of the side \(\displaystyle BC\), we have

\(\displaystyle BC\cdot BM + CB\cdot CM = BC\cdot(BM+MC) = BC^2 = BD\cdot BA+CE\cdot CA. \)

Choose \(\displaystyle M\) such that \(\displaystyle BC\cdot BM=BD\cdot BA\); then \(\displaystyle CB\cdot CM = CE\cdot CA\) is automaticaly satisfied. (Sice \(\displaystyle BM=\frac{BC\cdot BM}{BC} < \frac{BC^2}{BC} = BC\), the point \(\displaystyle M\) lies inside the segment \(\displaystyle BC\).)

By \(\displaystyle BC\cdot BM=BD\cdot BA\) and \(\displaystyle CB\cdot CM = CE\cdot CA\), the quadrilaterals \(\displaystyle ABME\) and \(\displaystyle ADMC\) are cyclic.

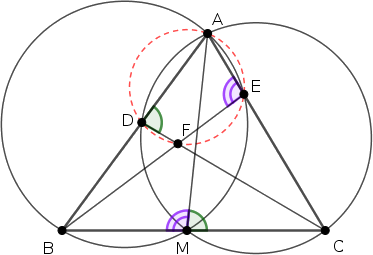
In the quadrilateral \(\displaystyle ADFE\) we have

\(\displaystyle ADF\sphericalangle+FEA\sphericalangle = AMC\sphericalangle+BMA\sphericalangle = 180^\circ,\)

that shows that the quadrilateral \(\displaystyle ADFE\) is cyclic.

Statistics:

36 students sent a solution.
5 points:	Baski Bence, Beke Csongor, Csaplár Viktor, Dobák Dániel, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Győrffy Ágoston, Hegedűs Dániel, Hervay Bence, Hoffmann Balázs, Jánosik Áron, Kerekes Anna, Kerekes Boldizsár, Kiss 014 Dávid, Kocsis Anett, Kovács 129 Tamás, Markó Gábor, Márton Dénes, Mátravölgyi Bence, Nguyen Bich Diep, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Weisz Máté.
4 points:	Nguyễn Minh Khang, Szabó 991 Kornél.
3 points:	1 student.
2 points:	2 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, October 2018