A B. 4982. feladat (2018. november)

B. 4982. Az \(\displaystyle ABCD\) konvex deltoid \(\displaystyle AC\) és \(\displaystyle BD\) átlói az \(\displaystyle E\) pontban metszik egymást úgy, hogy \(\displaystyle AE<CE\). Az \(\displaystyle AC\) átló felezőpontja \(\displaystyle F\). Az \(\displaystyle ABE\) és \(\displaystyle CDE\) körök második, \(\displaystyle E\)-től különböző metszéspontja \(\displaystyle M\). Mutassuk meg, hogy \(\displaystyle EMF\sphericalangle=90^\circ\).

(3 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. Legyen az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle K\), a \(\displaystyle CD\) oldal felezőpontja \(\displaystyle L\), továbbá legyen az \(\displaystyle EF\) szakasz felezőpontja \(\displaystyle N\).

Vegyük észre, hogy az \(\displaystyle N\) pont egyben a \(\displaystyle KL\) szakasz felezőpontja is, mert

\(\displaystyle \overrightarrow{EK}+\overrightarrow{EL} = \dfrac{\overrightarrow{EA}+\overrightarrow{EB}}2 + \dfrac{\overrightarrow{EC}+\overrightarrow{ED}}2 = \dfrac{\overrightarrow{EA}+\overrightarrow{EC}}2 = \overrightarrow{EF} = 2\overrightarrow{EN}. \)

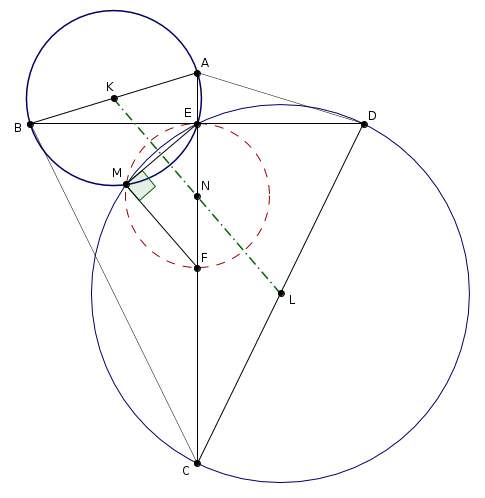
Most tekintsük az \(\displaystyle ABE\), \(\displaystyle CDE\) köröket, és az \(\displaystyle EF\) szakasz Thalész-körét. A deltoid átlói merőlegesen metszik egymást, tehát az \(\displaystyle ABE\) és \(\displaystyle CDE\) háromszögek derékszögűek. A Thalész-tétel megfordítása szerint az első két kör középpontja \(\displaystyle K\), illetve \(\displaystyle L\); a harmadik kör középpontja \(\displaystyle N\). Mint láttuk, ez a három középpont egy egyenesre esik, így a \(\displaystyle KNL\) egyenesre mindhárom kör szimmetrikus. Mindhárom kör átmegy az \(\displaystyle E\) ponton, ezért átmenek az \(\displaystyle E\) pontnak a közös szimmetriatengelyre vonatkozó tükörképén is, ami tehát az \(\displaystyle M\) pont.

Tehát az \(\displaystyle EF\) szakasz Thalész-köre átmegy az \(\displaystyle M\) ponton; ez bizonyítja, hogy \(\displaystyle EMF\sphericalangle\) derékszög.

Statisztika:

66 dolgozat érkezett.
3 pontot kapott:	Al-Hag Máté Amin, Argay Zsolt, Bánó Bulcsú, Baski Bence, Bauer Lujza, Beke Csongor, Bencsik Ádám, Csaplár Viktor, Csertán András, Dobák Dániel, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Győrffy Johanna, Hámori Janka, Hervay Bence, Jánosik Máté, Kerekes Anna, Kerekes Boldizsár, Kitschner Bernadett, Kovács 129 Tamás, Lengyel Ádám, Lovas Márton, Markó Gábor, Mátravölgyi Bence, Nagy Nándor, Nguyen Bich Diep, Rareș Polenciuc, Révész Máté, Richlik Róbert, Sebestyén Pál Botond, Seres-Szabó Márton, Snehansu Bhowmick, Szabó 417 Dávid, Telek Zsigmond , Terjék András József, Tiderenczl Dániel, Tiszay Dávid, Tóth Ábel, Várkonyi Zsombor, Velich Nóra, Vida Tamás, Weisz Máté.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2018. novemberi matematika feladatai