A B. 4985. feladat (2018. november)

B. 4985. Adott négy egyenes úgy, hogy közülük bármelyik három meghatároz egy háromszöget. Bizonyítsuk be, hogy ennek a négy háromszögnek a magasságpontja egy egyenesre illeszkedik.

(5 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldásvázlat. Először azt látjuk be, hogy a négy háromszög körülírt körének van közös pontja. Legyen a 4 megadott egyenes \(\displaystyle AB\), \(\displaystyle AC\), \(\displaystyle BD\) és \(\displaystyle CD\); az általuk meghatározott háromszögek pedig \(\displaystyle ABE\), \(\displaystyle ECD\), \(\displaystyle AFC\) és \(\displaystyle BFD\). Legyen továbbá az \(\displaystyle ABE\) és \(\displaystyle ECD\) háromszögek körülírt köreinek második metszéspontja \(\displaystyle M\). Megmutatjuk, hogy az \(\displaystyle M\) pont mind a négy kör közös pontja. Elegendő megmutatni, hogy az \(\displaystyle AFC\) háromszög körülírt köre illeszkedik az \(\displaystyle M\) pontra, a \(\displaystyle BFD\) háromszögre a bizonyítás ugyanezekkel a lépésekkel leírható. Azt kell megmutatni, hogy \(\displaystyle AFCM\) húrnégyszög. A feltételek alapján \(\displaystyle ECDM\) és \(\displaystyle ABEM\) húrnégyszögek, így az ábrán megjelölt szögek egyenlők: \(\displaystyle MED\sphericalangle=MCD\sphericalangle\), mert az \(\displaystyle MD\) íven nyugvó kerületi szögek, továbbá \(\displaystyle MAB\sphericalangle=MED\sphericalangle\), mert az \(\displaystyle MABE\) húrnégyszög szemközti belső, illetve külső szögei.

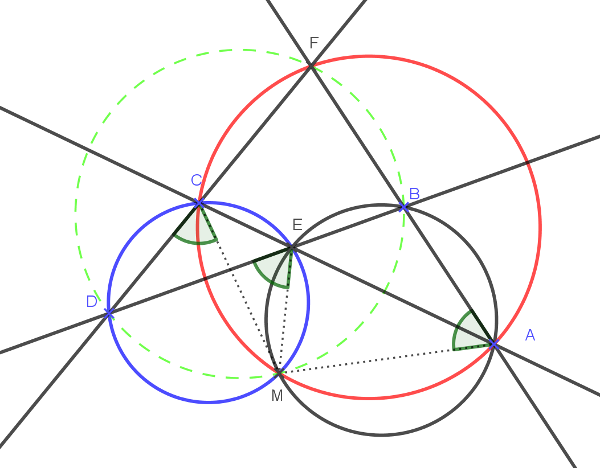
Tehát a négy körülírt körnek van közös pontja. Állítsunk most ebből a pontból az oldalegyenesekre merőlegeseket. A Simson-egyenesre vonatkozó tétel alapján tudjuk, hogy ezek a talppontok egy egyenesre illeszkednek.

Az is ismert, több helyen szereplő feladat, hogy a háromszög magasságpontján átmenő tetszőleges \(\displaystyle e\) egyenesnek a háromszög oldalaira vonatkozó tükörképei a körülírt körön metszik egymást. Ennek igazolásához elegendő megmutatni, hogy a tükrözött egyenesek közül bármelyik kettő a körülírt körön metszi egymást, mivel az egyik körrel alkotott metszéspont minden esetben a magasságpontnak az oldalra vonatkozó tükörképe. Legyenek az \(\displaystyle M\) magasságpontnak az oldalakra vonatkozó tükörképei \(\displaystyle M_1\), \(\displaystyle M_2\), az \(\displaystyle e\) egyenes oldalakra vonatkozó tükörképei pedig \(\displaystyle e_1\) és \(\displaystyle e_2\).

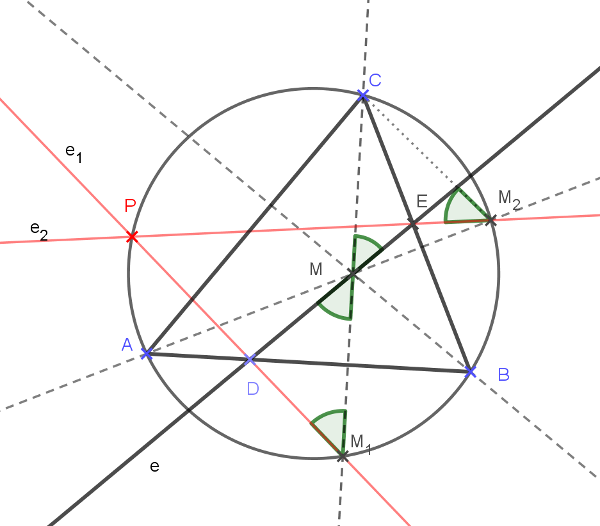
A tükrözések miatt az ábrán jelölt szögek egymással mind egyenlők. Az \(\displaystyle M_1\) és \(\displaystyle M_2\) pontokból a \(\displaystyle C\) csúcs és az \(\displaystyle e_1\), \(\displaystyle e_2\) egyenesek \(\displaystyle P\) metszéspontja ugyanakkora szögben látszanak, tehát \(\displaystyle P\) is az \(\displaystyle M_1\), \(\displaystyle M_2\) és \(\displaystyle C\) pontokat tartalmazó körön, a körülírt körön van.

Ha ebből a \(\displaystyle P\) pontból az oldalegyenesekre merőlegeseket állítunk, majd a \(\displaystyle P\) pontot sorra ezekre a talppontokra tükrözzük, akkor visszajutunk ahhoz az egyeneshez, amelynek tükörképei metszéseként ezt a pontot kaptuk – vagyis a \(\displaystyle P\) tükörképei egy, a magasságponton átmenő egyenesen sorakoznak. Ehhez az egyeneshez úgy is eljuthatunk, ha a \(\displaystyle P\) pontból a hozzátartozó Simson-egyenesre \(\displaystyle \lambda=2\) arányú középpontos hasonlóságot alkalmazunk. Ez az egyenes átmegy a háromszög magasságpontján.

A feladat befejezéseként alkalmazzuk a négy kör közös \(\displaystyle M\) pontjához tartozó Simson-egyenesre ezt a hasonlóságot. Egy egyenest kapunk, amely mind a négy magasságpontra illeszkedik.

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Apagyi Dávid, Beke Csongor, Bencsik Ádám, Csaplár Viktor, Csiszár Zoltán, Fekete Richárd, Fülöp Anna Tácia, Geretovszky Anna, Győrffi Ádám György, Győrffy Ágoston, Hegedűs Dániel, Jánosik Áron, Keltai Dóra, Kerekes Anna, Kerekes Boldizsár, Kitschner Bernadett, Kovács 343 Botond, Markó Gábor, Nagy Nándor, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Tiderenczl Dániel, Weisz Máté.
4 pontot kapott:	Tubak Dániel.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2018. novemberi matematika feladatai