 |
A B. 4989. feladat (2018. november) |
B. 4989. Az \(\displaystyle ABC\) háromszög \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalainak felezőpontjai rendre \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Jelölje a háromszög súlypontját \(\displaystyle S\). Tegyük fel, hogy az \(\displaystyle AFS\), \(\displaystyle BDS\) és \(\displaystyle CES\) háromszögek kerülete egyenlő. Mutassuk meg, hogy az \(\displaystyle ABC\) háromszög szabályos.
(6 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. Legyen az oldalak hossza \(\displaystyle BC=2a\), \(\displaystyle CA=2b\) és \(\displaystyle AB=2c\); a súlyvonalak hossza \(\displaystyle AD=3x\), \(\displaystyle BE=3y\), \(\displaystyle CF=3z\).
Mint jól ismert, a \(\displaystyle BCS\) háromszögben az \(\displaystyle SD\) súlyvonalra \(\displaystyle 4SD^2=2SB^2+2SC^2-BC^2\), azaz \(\displaystyle 4x^2=8y^2+8y^2-4a^2\); ebből azt kapjuk, hogy \(\displaystyle a=\sqrt{2y^2+2z^2-x^2}\). Hasonlóan, \(\displaystyle b=\sqrt{2x^2+2z^2-y^2}\) és \(\displaystyle c=\sqrt{2x^2+2y^2-z^2}\).
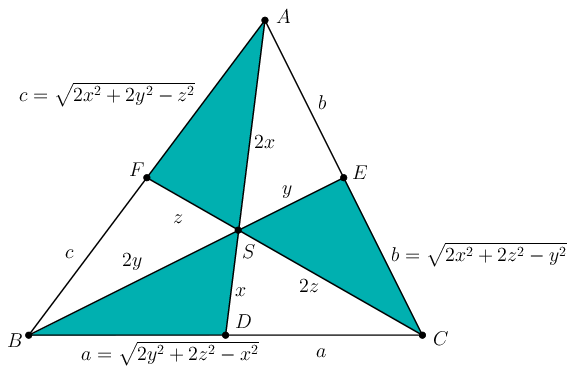
A feltétel szerint az \(\displaystyle AFS\) és \(\displaystyle CES\) háromszögek kerülete egyenlő:
\(\displaystyle k_{AFS} = 2x+z+c = x+2y+a = k_{CES}, \)
\(\displaystyle 2x+z+\sqrt{2x^2+2y^2-z^2} = y+2z+\sqrt{2z^2+2z^2-y^2}. \)
Azért, hogy megszabaduljunk a gyökjelektől, rendezzük egy oldalra a négyzetgyököket, majd emeljünk négyzetre:
\(\displaystyle 2x-y-z = \sqrt{2x^2+2z^2-y^2}-\sqrt{2x^2+2y^2-z^2}, \)
\(\displaystyle 4x^2+y^2+z^2-4xy-4xz+2yz = (2x^2+2z^2-y^2) -2\sqrt{2x^2+2z^2-y^2}\sqrt{2x^2+2y^2-z^2} +(2x^2+2y^2-z^2) . \)
Rendezzük ismét egy oldalra a négyzetgyököket (közben \(\displaystyle 2\)-vel oszthatunk), és emeljünk négyzetre:
\(\displaystyle \sqrt{2x^2+2z^2-y^2}\sqrt{2x^2+2y^2-z^2} = 2xy+2xz-yz, \)
\(\displaystyle 4x^4-2y^4-2z^4+2x^2y^2+2x^2z^2+5y^2z^2 = 4x^2y^2+4x^2z^2+y^2z^2+8x^2yz-4xy^2z-4xyz^2 . \)
Ezt megint egy oldalra rendezzük és \(\displaystyle 2\)-vel osztunk:
| \(\displaystyle 2x^4-y^4-z^4-x^2y^2-x^2z^2+2y^2z^2-4x^2yz+2xy^2z+2xyz^2 = 0. \) | \(\displaystyle (1) \) |
Az \(\displaystyle x,y,z\) és \(\displaystyle a,b,c\) ciklikus cseréjével ugyanígy kaphatjuk, hogy
| \(\displaystyle 2y^4-z^4-x^4-y^2z^2-y^2x^2+2z^2x^2-4y^2zx+2yz^2x+2yzx^2 = 0 \) | \(\displaystyle (2) \) |
és
| \(\displaystyle 2z^4-x^4-y^4-z^2x^2-z^2y^2+2x^2y^2-4z^2xy+2zx^2y+2zxy^2 = 0. \) | \(\displaystyle (3) \) |
Vegyük az (1) és (2) különbségét. Ebből \(\displaystyle x-y\) kiemelhető:
\(\displaystyle 3x^4-3y^4-3x^2z^2+3y^2z^2-6x^2yz+6xy^2z = 0, \)
| \(\displaystyle 3(x-y)(x^3+x^2y+xy^2+y^3-xz^2-yz^2-2xyz) = 0. \) | \(\displaystyle (4) \) |
Hasonlóan, a (2) és (3) különbségéből
| \(\displaystyle 3(y-z)(y^3+y^2z+yz^2+z^3-yx^2-zx^2-2xyz) = 0. \) | \(\displaystyle (5) \) |
A ciklikus szimmetria miatt feltehetjük, hogy \(\displaystyle x,y,z\) közül \(\displaystyle y\) az (egyik) középső, azaz \(\displaystyle x\) és \(\displaystyle z\) az egyik legkisebb és a legnagyobb valamilyen sorrendben.
Vizsgáljuk (4) második tényezőjét. Ha \(\displaystyle x,y,z\) közül \(\displaystyle z\) a legkisebb, azaz \(\displaystyle z\le x\) és \(\displaystyle z\le y\), akkor
\(\displaystyle x^3+x^2y+xy^2+y^3-xz^2-yz^2-2xyz = x(x^2-z^2) + xy(x-z) + xy(y-z) + y^2(y-z) \ge 0, \)
és egyenlőség csak akkor áll, ha \(\displaystyle z=x\) és \(\displaystyle z=y\) is teljesül. Hasonlóan, ha \(\displaystyle z\) a legnagyobb, akkor
\(\displaystyle x^3+x^2y+xy^2+y^3-xz^2-yz^2-2xyz \le 0, \)
és egyenlőség megint csak \(\displaystyle x=y=z\) esetén lehet. Tehát (feltéve, hogy \(\displaystyle x,y,z\) közül \(\displaystyle z\) a legkisebb vagy a legnagyobb) a (4) egyenlet csak úgy teljesülhet, ha \(\displaystyle x=y\).
Ugyanígy, (5) csak akkor teljesül, ha \(\displaystyle y=z\).
Tehát biztosan \(\displaystyle x=y=z\), vagyis \(\displaystyle a=b=c\), és a háromszög szabályos.
Statisztika:
46 dolgozat érkezett. 6 pontot kapott: Baski Bence, Bursics András, Dobák Dániel, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Győrffy Johanna, Hegedűs Dániel, Kitschner Bernadett, Nagy Nándor, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Terjék András József, Török Mátyás, Velich Nóra, Weisz Máté, Zsigri Bálint. 5 pontot kapott: Beke Csongor, Fleiner Zsigmond, Győrffy Ágoston, Jánosik Áron, Kerekes Anna, Tóth-Rohonyi Iván. 4 pontot kapott: 4 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 10 versenyző.
A KöMaL 2018. novemberi matematika feladatai

