 |
A B. 4996. feladat (2018. december) |
B. 4996. Adott egy szakasz és az egyik harmadolópontja. Szerkesszük meg csak vonalzó segítségével a másik harmadolópontot.
(6 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Legyen \(\displaystyle AB\) a megadott szakasz, és \(\displaystyle H\) az \(\displaystyle A\)-hoz közelebbi harmadolópontja; ezekből szeretnénk megszerkeszteni a \(\displaystyle B\)-hez közelebbi harmadolópontot, amely egyben a \(\displaystyle BH\) szakasz felezőpontja.
Vegyünk fel az \(\displaystyle AB\) egyenesen kívül egy \(\displaystyle C\) pontot, és a \(\displaystyle CH\) szakaszon egy \(\displaystyle D\) pontot. Szerkesszük meg az \(\displaystyle E=AD\cap BC\) és \(\displaystyle F=AC\cap BD\), majd a \(\displaystyle T=AB\cap EF\) pontot. Írjuk fel a Ceva- és a Menelaosz-tételt az \(\displaystyle ABC\) háromszögben a \(\displaystyle D\) pontra, illetve az \(\displaystyle EFT\) egyenesre:
\(\displaystyle \frac{AH}{HB} \cdot \frac{BE}{EC} \cdot \frac{CF}{FA} = 1, \quad\text{illetve}\quad \frac{AT}{TB} \cdot \frac{BE}{EC} \cdot \frac{CF}{FA} = -1, \)
amiből
\(\displaystyle \frac{AT}{TB} = -\frac{AH}{HB} = -\frac12. \)
Az arány negatív, tehát a \(\displaystyle T\) pont az \(\displaystyle AB\) szakaszon kívülre esik, és \(\displaystyle TA=\frac12TB\), vagyis \(\displaystyle A\) a \(\displaystyle TB\) szakasz felezőpontja.
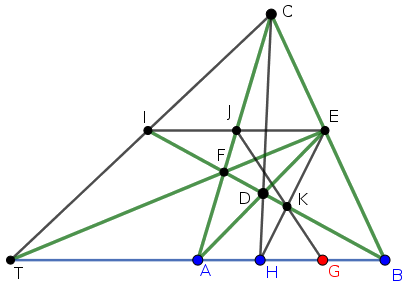
Ezek után legyen \(\displaystyle I=BD\cap CT\). Az \(\displaystyle BCT\) háromszögre és az \(\displaystyle F\) pontra felírva a Ceva-tételt:
\(\displaystyle \frac{BE}{EC}\cdot\frac{CI}{IT}\cdot\frac{TA}{AB} = \frac{BE}{EC}\cdot\frac{CI}{IT} = 1, \)
vagyis \(\displaystyle \frac{CE}{EB}=\frac{CI}{IT}\); a párhuzamos szelők tételének megfordítása szerint \(\displaystyle EI\) párhuzamos \(\displaystyle AB\)-vel.
Most szerkesszük meg a \(\displaystyle J=AC\cap EI\), \(\displaystyle K=BI\cap EH\), végül a \(\displaystyle G=AB\cap JK\) pontokat. Mivel a \(\displaystyle TAGB\) és \(\displaystyle EJI\) egyenesek párhuzamosak, abból, hogy \(\displaystyle TB\) felezőpontja \(\displaystyle A\), az \(\displaystyle F\) ponton keresztül vetítve látjuk, hogy \(\displaystyle EI\) felezőpontja \(\displaystyle J\); a \(\displaystyle K\) ponton keresztül visszavetítve az \(\displaystyle AB\) egyenesre, láthatjuk, hogy \(\displaystyle HB\) felezőpontja \(\displaystyle G\), ami éppen az \(\displaystyle AB\) szakasz másik, \(\displaystyle B\)-hez közelebbi harmadolópontja.
A fenti szerkesztési eljárás tehát valóban a másik harmadolópontot szerkeszti meg.
Statisztika:
59 dolgozat érkezett. 6 pontot kapott: Argay Zsolt, Beke Csongor, Bencsik Ádám, Csaplár Viktor, Csiszár Zoltán, Dobák Dániel, Geretovszky Anna, Győrffi Ádám György, Győrffy Ágoston, Győrffy Johanna, Hámori Janka, Hegedűs Dániel, Hervay Bence, Hoffmann Balázs, Jánosik Áron, Kerekes Anna, Markó Gábor, Nádor Benedek, Nagy Nándor, Péter Kristóf, Pooya Esmaeil Akhoondy, Rareș Polenciuc, Richlik Róbert, Seres-Szabó Márton, Soós 314 Máté, Szabó 417 Dávid, Telek Zsigmond , Tóth 827 Balázs, Tóth Ábel, Várkonyi Zsombor, Weisz Máté, Zsigri Bálint. 5 pontot kapott: Biczó Benedek. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 16 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2018. decemberi matematika feladatai

