 |
A B. 4999. feladat (2019. január) |
B. 4999. Az \(\displaystyle ABC\) háromszög beírt körének középpontja \(\displaystyle O\), érintési pontjai \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), hozzáírt köreinek érintési pontjai \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\) az ábra szerint. Mutassuk meg, hogy az \(\displaystyle OA_1 A_2\), \(\displaystyle OB_1 B_2\) és \(\displaystyle OC_1 C_2\) háromszögek közül valamelyiknek a területe egyenlő a másik két háromszög területének összegével.
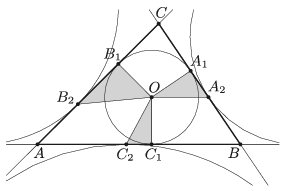
Javasolta: Kocsis Szilveszter (Budapest)
(3 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás. Először is állapítsuk meg, hogy, ha a háromszög szabályos, akkor az \(\displaystyle OA_1 A_2\), \(\displaystyle OB_1 B_2\) és \(\displaystyle OC_1 C_2\) háromszögek elfajuló háromszögek 0 területtel és így triviális az állítás, míg, ha a háromszög egyenlő szárú (de nem szabályos), akkor az alapon keletkező háromszög elfajuló, míg a másik két háromszög a szimmetria miatt egybevágó, és így ekkor is teljesül a feladat állítása.
Legyen most már \(\displaystyle a>b>c\) , és használjuk az alábbi ábra jelöléseit!

A körhöz közös külső pontból húzott érintőszakaszok egyenlő hossza miatt \(\displaystyle C_1A=AB_1 = x\), \(\displaystyle C_1B=BA_1 = y\), \(\displaystyle B_1C=CA_1=z\). Innen \(\displaystyle 2(x+y+z) = a+b+c=2s\), és \(\displaystyle BA_1 = y=s-(x+z)=s-b=\dfrac{a-b+c}{2}\).
Ugyanígy a körhöz közös külső pontból húzott érintőszakaszok egyenlő hossza miatt: \(\displaystyle QB=BA_2=q\) és \(\displaystyle A_2C=CP=p\), valamint \(\displaystyle AQ=AP=q+c=p+b=s\), és innen \(\displaystyle BA_2= q=s-c=\dfrac{a+b-c}{2}\).
Azaz \(\displaystyle A_1A_2=|BA_2 - BA_1|=\left|\dfrac{a-b+c}{2}-\dfrac{a+b-c}{2}\right|=|c-b| = b-c\) (\(\displaystyle b>c\) miatt).
Hasonlóan megmutatható, hogy \(\displaystyle B_1B_2=a-c\) és \(\displaystyle C_1C_2=a-b\).
Mivel a kérdéses \(\displaystyle OA_1 A_2\), \(\displaystyle OB_1 B_2\) és \(\displaystyle OC_1 C_2\) háromszögek derékszögűek, és az \(\displaystyle A_1A_2, B_1B_2, C_1C_2\) befogókhoz tartozó magasság minden esetben a beírható kör \(\displaystyle r\) sugara, adódik, hogy a nagyság szerint középső oldalon lévő \(\displaystyle OB_1B_2\) háromszögre:
\(\displaystyle 2T_{OB_1B_2} = (a-c)r=(a-b+b-c)r=(a-b)r + (b-c)r = 2T_{OC_1C_2} + 2T_{OA_1A_2}\).
Ezt kettővel osztva éppen a bizonyítandó állítást kapjuk.
Statisztika:
74 dolgozat érkezett. 3 pontot kapott: Apagyi Dávid, Baski Bence, Beke Csongor, Biczó Benedek, Bokor Endre, Bukva Dávid, Csaplár Viktor, Csizmadia Miklós, Dezső Kende Barnabás, Dobák Dániel, Fekete Richárd, Füredi Erik Benjámin, Gyetvai Miklós, Győrffi Ádám György, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Jánosik Máté, Kerekes Anna, Kerekes Boldizsár, Kinyó Kincső, Kitschner Bernadett, Kós Péter, Lovas Márton, Major Botond, Markó Gábor, Nagy Nándor, Nguyen Bich Diep, Pooya Esmaeil Akhoondy, Rareș Polenciuc, Sebestyén Pál Botond, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Szénás Anna Lilla, Szűcs 064 Tamás, Telek Zsigmond , Tiderenczl Dániel, Tiszay Dávid, Tóth 057 Bálint, Tóth 827 Balázs, Tóth Ábel, Török Ágoston, Tubak Dániel, Várkonyi Zsombor, Vida Tamás, Zsigri Bálint. 2 pontot kapott: 25 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2019. januári matematika feladatai

