 |
A B. 5001. feladat (2019. január) |
B. 5001. Egy egyenlő szárú háromszög alapja \(\displaystyle a\), szárszöge \(\displaystyle 120^{\circ}\)-nál kisebb, az alaphoz tartozó magassága \(\displaystyle m\). A háromszög mindegyik csúcsát tükrözzük a szemközti oldalegyenesre. A három kapott pont egy másik egyenlő szárú háromszöget alkot, amelynek alapja \(\displaystyle a'\), alaphoz tartozó magassága pedig \(\displaystyle m'\). Mutassuk meg, hogy
\(\displaystyle \frac{a'}{a}+\frac{m'}{m}=4. \)
Javasolta: Bártfai Pál (Budapest)
(3 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás. Legyen a háromszög alapja \(\displaystyle BC\), szárainak metszéspontja \(\displaystyle A\), a tükörképpontok pedig \(\displaystyle A', B', C'\).
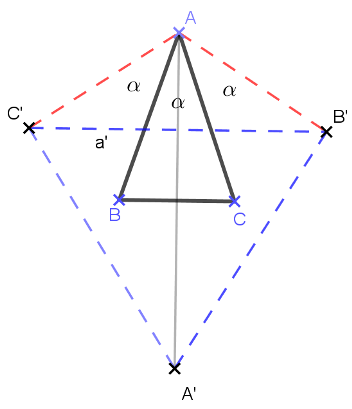
Az általánosság megszorítása nélkül vehetjük a szárakat egységnyinek. Az összes adat kifejezhető a szár és a szárak közötti \(\displaystyle \alpha\) szög segítségével. A kényelmesebb írás érdekében legyen továbbá \(\displaystyle \frac{\alpha}{2}=\varphi\):
\(\displaystyle a=BC=2\sin\varphi,\)
\(\displaystyle m=\cos\varphi,\)
\(\displaystyle a'=2\sin 3\varphi,\)
\(\displaystyle m'=2\cos\varphi-\cos 3\varphi.\)
A háromszoros szögekre vonatkozó addíciós tételek és a négyzetes összefüggés segítségével írjuk fel a megfelelő szakaszok arányát:
\(\displaystyle \frac{a'}{a}+\frac{m'}{m}=\frac{2\sin\varphi(3-4\sin^2 \varphi)}{2\sin\varphi}+ \frac {2\cos\varphi - \cos\varphi(4\cos^2\varphi-3)}{\cos\varphi}=\)
\(\displaystyle =3-4\sin^2\varphi+2-4\cos^2\varphi+3=8-4(\sin^2\varphi+\cos^2\varphi)=4. \)
Amennyiben \(\displaystyle 3\alpha\) nagyobb, mint \(\displaystyle 180^{\circ}\), a félszöge még mindig kisebb \(\displaystyle 180^{\circ}\)-nál, így a szinuszok számolásánál ez nem okoz problémát. A félszög koszinusza viszont negatív lesz, ami éppen meg is felel, mert \(\displaystyle m'\) nagyobb ebben az esetben \(\displaystyle m\) kétszeresénél. Az algebrai felírás ekkor is pontos.
Statisztika:
59 dolgozat érkezett. 3 pontot kapott: Apagyi Dávid, Argay Zsolt, Bánó Bulcsú, Baski Bence, Bencsik Ádám, Bokor Endre, Bukva Dávid, Bursics András, Csaplár Viktor, Dobák Dániel, Fekete Richárd, Fraknói Ádám, Fülöp Anna Tácia, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Győrffy Johanna, Hámori Janka, Hamvas Johanna Kata, Hegedűs Dániel, Kerekes Anna, Kerekes Boldizsár, Kiss 014 Dávid, Kitschner Bernadett, Laki Anna, Lipthay Hanna, Lovas Márton, Markó Gábor, Mátravölgyi Bence, Nguyen Bich Diep, Rareș Polenciuc, Sándor Péter, Sebestyén Pál Botond, Szabó 417 Dávid, Szabó 991 Kornél, Telek Zsigmond , Tiderenczl Dániel, Várkonyi Zsombor, Velich Nóra. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2019. januári matematika feladatai

