Problem B. 5008. (February 2019)

B. 5008. A circle \(\displaystyle k_A\) is centred at \(\displaystyle A\), and a circle \(\displaystyle k_B\) is centred at \(\displaystyle B\). Line \(\displaystyle l_1\) touches \(\displaystyle k_A\) at \(\displaystyle A_1\) and \(\displaystyle k_B\) at \(\displaystyle B_1\). Line \(\displaystyle l_2\) touches \(\displaystyle k_A\) at \(\displaystyle A_2\) and \(\displaystyle k_B\) at \(\displaystyle B_2\). Prove that the orthogonal projections of the line segments \(\displaystyle A_1A_2\) and \(\displaystyle B_1B_2\) onto the line \(\displaystyle AB\) are of equal length.

(3 pont)

Deadline expired on March 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Amennyiben két külső vagy két belső érintőt húztunk be, a megfelelő pontok vetületei egybeesnek, nincs mit bizonyítanunk. A feladat valódi állítása arra az esetre vonatkozik, ha mindkét körhöz húzható külső és belső érintő is és az egyik egyenes külső, a másik belső érintő. Legyen \(\displaystyle l_1\) a közös külső, \(\displaystyle l_2\) pedig a közös belső érintő.

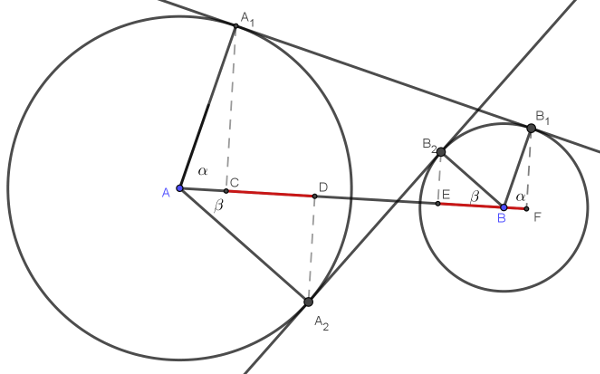
Legyenek az \(\displaystyle A_1, A_2, B_2, B_1\) pontok merőleges vetületének talppontjai az \(\displaystyle AB\) egyenesen rendre a \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) pontok. Legyen \(\displaystyle k_A\) sugara \(\displaystyle R\), \(\displaystyle k_B\) sugara \(\displaystyle r\), a középpontok távolsága \(\displaystyle AB=d\), \(\displaystyle BAA_1 \measuredangle=\alpha\), \(\displaystyle A_2AB\measuredangle=\beta\). Az ismert szerkesztési eljárás alapján a \(\displaystyle B\) pontból az \(\displaystyle AA_1\) szakaszra merőlegest állítva látható, hogy

\(\displaystyle \cos\alpha=\frac{R-r}{d}.\)

Ismét a szerkesztési eljárás alapján \(\displaystyle B\)-ből az \(\displaystyle AA_2\) egyenesére merőlegest állítva adódik, hogy

\(\displaystyle \cos\beta=\frac{R+r}{d}.\)

A külső és belső érintő elhelyezkedése alapján az \(\displaystyle A_1\) pont és az \(\displaystyle A_2\) pont vetülete is az \(\displaystyle AB\) szakaszra esik, mégpedig úgy, hogy a \(\displaystyle D\) pont van távolabb az \(\displaystyle A\)-tól, mint \(\displaystyle C\). Fel tudjuk írni az eddigiek alapján a \(\displaystyle CD\) vetületszakasz hosszát:

\(\displaystyle CD=R\cos\beta-R\cos\alpha=R\cdot\frac{R+r}{d}-R\cdot\frac{R-r}{d}=\frac{2Rr}{d}.\)

Feltettük, hogy \(\displaystyle R>r\), ezért a \(\displaystyle B_1\) pont \(\displaystyle F\) vetülete az \(\displaystyle AB\) szakasz \(\displaystyle B\)-n túli meghosszabbítására esik. A szögfüggvények értékeinek felhasználásával felírható az \(\displaystyle EF\) szakasz hossza:

\(\displaystyle EF=r\cos\alpha+r\cos\beta=r\cdot\frac{R-r}{d}+r\cdot\frac{R+r}{d}=\frac{2Rr}{d}.\)

Amennyiben a körök kívülről érintik egymást, akkor a \(\displaystyle D\) és \(\displaystyle E\) pontok egymással és a két kör közös pontjával is egybeesnek. A \(\displaystyle \beta\) szög \(\displaystyle 0^\circ\)-os, így \(\displaystyle \cos\beta=1\), \(\displaystyle R\cos\beta=R, r\cos\beta=r\), ebben az esetben is ugyanezzel számolással kapjuk a vetületek hosszát. Ezzel az állítást igazoltuk.

Statistics:

45 students sent a solution.
3 points:	Apagyi Dávid, Bánó Bulcsú, Baski Bence, Beke Csongor, Biczó Benedek, Csaplár Viktor, Fekete Richárd, Füredi Erik Benjámin, Geretovszky Anna, Győrffy Johanna, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kerekes Anna, Kitschner Bernadett, Lovas Márton, Rareș Polenciuc, Sándor Péter, Sárvári Tibor, Soós 314 Máté, Telek Zsigmond , Tiderenczl Dániel, Tóth 057 Bálint, Tóth Ábel, Velich Nóra.
2 points:	Laki Anna, Markó Gábor, Nagy 551 Levente, Nguyen Bich Diep, Osztényi József, Richlik Róbert.
1 point:	1 student.
0 point:	13 students.

Problems in Mathematics of KöMaL, February 2019