 Problem B. 5016. (March 2019)
Problem B. 5016. (March 2019)
B. 5016. In a convex quadrilateral \(\displaystyle ABCD\), point \(\displaystyle E_1\) lies on side \(\displaystyle AD\), point \(\displaystyle F_1\) lies on side \(\displaystyle BC\), \(\displaystyle E_2\) lies on diagonal \(\displaystyle AC\), and \(\displaystyle F_2\) lies on diagonal \(\displaystyle BD\). Given that
\(\displaystyle AE_1:E_1D=BF_1:F_1C=AE_2:E_2C=BF_2:F_2D=AB:CD. \)
and no pair of points coincide, prove that the lines \(\displaystyle E_1F_1\) and \(\displaystyle E_2F_2\) are perpendicular.
(4 pont)
Deadline expired on April 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen \(\displaystyle AB=x\) és \(\displaystyle CD=y\). A feltétel szerint az \(\displaystyle E_1\) és az \(\displaystyle F_2\) pontok a \(\displaystyle DA\), illetve \(\displaystyle DB\) szakaszokat \(\displaystyle y:x\) arányban osztják, ezért \(\displaystyle \frac{DE_1}{DA}=\frac{DF_2}{DB}=\frac{y}{x+y}\). Ha az \(\displaystyle AB\) szakaszt a \(\displaystyle D\) pontból \(\displaystyle \frac{y}{x+y}\)-szorosára kicsinyítjük, éppen az \(\displaystyle E_1E_2\) szakaszt kapjuk. Ezért az \(\displaystyle E_1E_2\) szakasz hossza
\(\displaystyle E_1F_2 = \frac{y}{x+y}\cdot AB = \frac{y}{x+y}\cdot x = \frac{xy}{x+y}.\)
Hasonlóan, az \(\displaystyle AB\) szakaszt a \(\displaystyle C\)-ból \(\displaystyle \frac{y}{x+y}\)-szorosára, a \(\displaystyle CD\) szakaszt \(\displaystyle A\)-ból és \(\displaystyle B\)-ből \(\displaystyle \frac{x}{x+y}\)-szorosára kicsinyítve kapjuk, hogy \(\displaystyle E_2F_1=E_1E_2=F_1F_2=\frac{xy}{x+y}\).
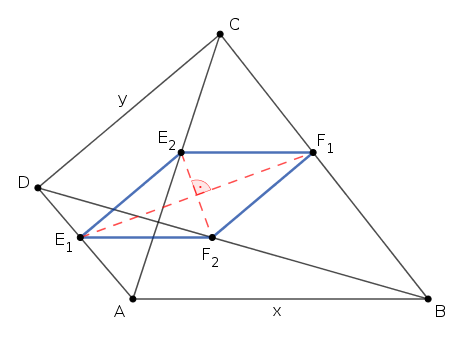
Mint látjuk, az \(\displaystyle E_1E_2F_1F_2\) négyszög mindegyik oldala \(\displaystyle \frac{xy}{x+y}\) hosszúságú, az \(\displaystyle E_1E_2F_1F_2\) négyszög tehát egy rombusz. Akkor viszont az átlói, \(\displaystyle E_1F_1\) és \(\displaystyle E_2F_2\) merőlegesek egymásra.
Statistics:
48 students sent a solution. 4 points: Al-Hag Máté Amin, Balogh Zsófia, Baski Bence, Beke Csongor, Bognár 171 András Károly, Bukva Dávid, Csaplár Viktor, Fleiner Zsigmond, Fraknói Ádám, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Hámori Janka, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kerekes Boldizsár, Kiss 014 Dávid, Kitschner Bernadett, Kovács 129 Tamás, Laki Anna, Lovas Márton, Ludányi Levente, Mátravölgyi Bence, Nagy 551 Levente, Nagy Nándor, Nguyen Bich Diep, Osztényi József, Rareș Polenciuc, Sebestyén Pál Botond, Soós 314 Máté, Stomfai Gergely, Szabó 991 Kornél, Tálos Zoltán, Telek Zsigmond , Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Velich Nóra, Weisz Máté, Zsigri Bálint. 3 points: Csizmadia Miklós, Fekete Richárd. 2 points: 3 students.
Problems in Mathematics of KöMaL, March 2019
