Problem B. 5019. (March 2019)

B. 5019. The quadrilateral \(\displaystyle ABCD\) is cyclic. Given that \(\displaystyle AB+BC=AD+DC\) and \(\displaystyle BA+AC=BD+DC\), show that \(\displaystyle ABCD\) is a rectangle.

(6 pont)

Deadline expired on April 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit, az átlók legyenek \(\displaystyle AC=e=e_1+e_2\) és \(\displaystyle BD=f=f_1+f_2\). Vezessük be továbbá az \(\displaystyle x=ab+cd\), \(\displaystyle y=ac+bd\) és \(\displaystyle z=ad+bc\) jelöléseket.

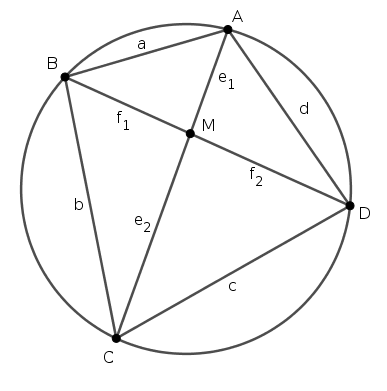
Először felidézünk néhány húrnégyszögekre vonatkozó állítást. A kerületi szögek tétele miatt \(\displaystyle ABD\angle=ACD\angle\) és \(\displaystyle CAB\angle=CDB\angle\), így \(\displaystyle ABM\triangle\sim CDM\triangle\). Ugyanígy \(\displaystyle BCM\triangle\sim DAM\triangle\), s a két hasonlóságból

\(\displaystyle \frac {f_1}{e_2}=\frac {e_1}{f_2}=\frac a c, \quad \text{valamint} \quad \frac {e_1}{f_1}=\frac {f_2}{e_2}=\frac d b.\)

A két egyenlőséget összevetve

\(\displaystyle \frac ac= \frac {e_1}{f_2}=\frac{df_1}{bf_2}, \quad \text{valamint} \quad \frac{a}{c}=\frac{f_1}{e_2}=\frac{be_1}{de_2}.\)

Innen \(\displaystyle e_1=e_2\cdot ad/bc\) és \(\displaystyle f_2=f_1\cdot cd/ab\), amiből

\(\displaystyle \frac ef=\frac {e_1+e_2}{f_1+f_2}=\frac {\frac{ad}{bc}+1}{1+\frac{cd}{ab}}\cdot \frac {e_2}{f_1}=\frac {\frac{ad}{bc}+1}{1+\frac{cd}{ab}}\cdot \frac ca=\frac{ad+bc}{ab+cd}=\frac{z}{x}.\)

Emlékeztetünk továbbá a Ptolemaiosz-tételre, amely szerint \(\displaystyle ef=ac+bd=y\). Az átlók arányára, illetve szorzatára vonatkozó formulákból következik, hogy \(\displaystyle e^2=yz/x\) és \(\displaystyle f^2=xy/z\).

Rátérünk a feladat megoldására. A feltételek szerint \(\displaystyle a+b=c+d\) és \(\displaystyle a+e=c+f\), azaz \(\displaystyle a-c=d-b=f-e\). Innen

\(\displaystyle a-c=f-e=f\left ( 1-\frac e f \right )=f\left (1-\frac{ad+bc}{ab+cd} \right )=\frac{f}{ab+cd}((ab+cd)-(ad+bc))=\frac f {x}(a-c)(b-d)=-\frac{f}{x}(a-c)^2.\)

Ha \(\displaystyle a-c=0\), akkor a feltételek szerint \(\displaystyle a=c\), \(\displaystyle b=d\) és \(\displaystyle e=f\), vagyis a négyszög olyan paralelogramma, amelynek átlói egyenlő hosszúak, azaz valóban téglalap.

Ha \(\displaystyle a-c\neq 0\), akkor oszthatunk vele, és kapjuk, hogy \(\displaystyle f=x/(b-d)=x/(c-a)\). Felhasználva az \(\displaystyle f^2=xy/z\) összefüggést nyerjük, hogy

\(\displaystyle \frac{xy}{z}=f^2=\frac{x}{b-d}\cdot \frac{x}{c-a}=\frac{x^2}{bc-ba-dc+da}=\frac{x^2}{z-x}.\)

Ezt \(\displaystyle x\neq0\)-val egyszerűsítve és rendezve \(\displaystyle y+z=yz/x\) adódik. Vegyük észre, hogy \(\displaystyle (a+b)^2=(a+b)(c+d)=y+z\), és \(\displaystyle e^2=yz/x\), azaz \(\displaystyle e=a+b\), amiből következően az \(\displaystyle ABC\triangle\) elfajuló, ami ellentmondás.

Ezzel a bizonyítást befejeztük.

Megjegyzés. Az \(\displaystyle a-c=-f/x\cdot (a-c)^2\) összefüggésből azonnal következik \(\displaystyle a\le c\). ``Csábító'' lenne itt azzal folytatni, hogy \(\displaystyle a\) és \(\displaystyle c\) szerepe szimmetrikus, ezért hasonlóan belátható, hogy \(\displaystyle c\le a\), amiből \(\displaystyle a=c\) következik, és az állítás adódik. Vegyük azonban észre, hogy \(\displaystyle a\) és \(\displaystyle c\) szerepe nem szimmetrikus. Az \(\displaystyle a+b=c+d\) két oldalán lévő oldalakat az \(\displaystyle e\) átló elválasztja, míg az \(\displaystyle f\) nem, ezért az \(\displaystyle e\) és \(\displaystyle f\) szerepe nem szimmetrikus. Így viszont az \(\displaystyle a+e=c+f\) feltétel miatt \(\displaystyle a\) és \(\displaystyle c\) szerepe sem lehet szimmetrikus.

Statistics:

45 students sent a solution.
6 points:	Balogh Zsófia, Baski Bence, Beke Csongor, Bencsik Ádám, Bursics András, Csaplár Viktor, Csizmadia Miklós, Farkas Boróka, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Hegedűs Dániel, Jánosik Áron, Kitschner Bernadett, Kovács 129 Tamás, Kovács Alex, Le Julianna Phuonglinh, Nagy Nándor, Nguyen Bich Diep, Osztényi József, Rareș Polenciuc, Sebestyén Pál Botond, Soós 314 Máté, Stomfai Gergely, Szabó 991 Kornél, Tálos Zoltán, Telek Zsigmond , Terjék András József, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Trombitás Karolina Sarolta, Várkonyi Zsombor, Weisz Máté, Zsigri Bálint.
5 points:	Hervay Bence, Tiefenbeck Flórián, Velich Nóra.
4 points:	2 students.
0 point:	3 students.

Problems in Mathematics of KöMaL, March 2019