Problem B. 5028. (April 2019)

B. 5028. Let us define a function \(\displaystyle f\) as follows. For any acute-angled triangle \(\displaystyle XYZ\), if \(\displaystyle P\) is a point on \(\displaystyle YZ\), then \(\displaystyle f(P;XYZ)\) is defined as the line joining the feet of perpendiculars from \(\displaystyle P\) to lines \(\displaystyle XY\); \(\displaystyle XZ\).

Let \(\displaystyle ABC\) be a triangle with orthocenter \(\displaystyle H\). Let \(\displaystyle A'B'C'\) be the orthic triangle of \(\displaystyle ABC\). Let \(\displaystyle A''\equiv f(B';HCA) \cap f(C';HAB)\). Similarly, points \(\displaystyle B''\); \(\displaystyle C''\) are defined. Show that the lines \(\displaystyle AA''\); \(\displaystyle BB''\); \(\displaystyle CC''\) are concurrent.

Proposed by K. V. Sudharshan

(6 pont)

Deadline expired on May 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Először tegyük fel, hogy \(\displaystyle ABC\) hegyesszögű. Legyenek az \(\displaystyle A'B'C'\) megfelelő oldalfelező pontjai \(\displaystyle F_A\) és \(\displaystyle F_B\) az ábra szerint, és messe \(\displaystyle F_AF_B\) az \(\displaystyle AA'\) magasságot \(\displaystyle I\)-ben. Először megmutatjuk, hogy \(\displaystyle A''=F_A\) és \(\displaystyle B''=F_B\).

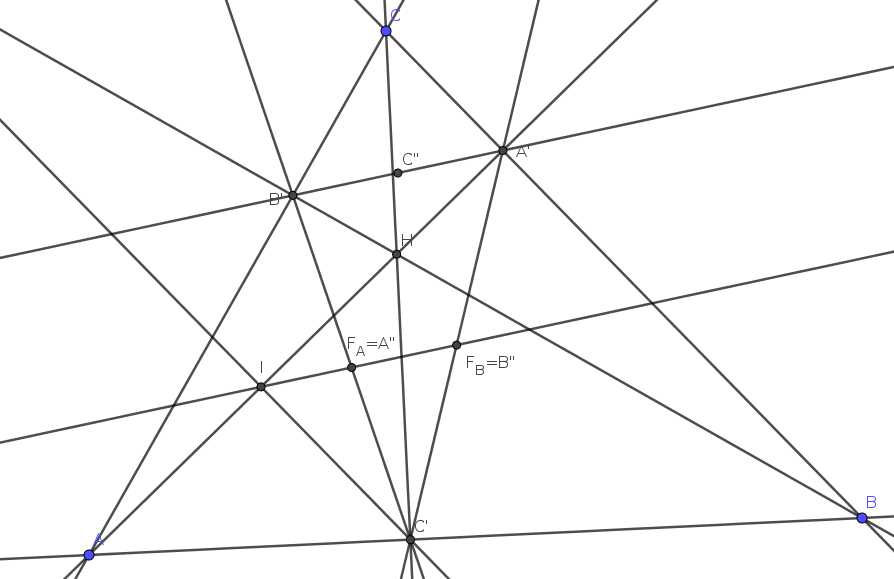
Az \(\displaystyle ABA'B'\) és \(\displaystyle ACA'C'\) négyszögek húrnégyszögek, mert az \(\displaystyle A'\) és \(\displaystyle B'\) pontok, ill. az \(\displaystyle A'\) és \(\displaystyle C'\) pontok a Thalész-tétel megfordítása miatt illeszkednek az \(\displaystyle AB\), ill. \(\displaystyle AC\) szakaszok Thalész-körére. A két húrnégyszög \(\displaystyle A'\)-nél lévő külső szögeire \(\displaystyle B'A'C\angle=C'A'B\angle=\alpha\). Ebből azonnal következik, hogy \(\displaystyle IA'F_B\angle=90^{\circ}-\alpha\), és mivel \(\displaystyle A'B'\parallel F_AF_B\), így \(\displaystyle IF_BA'\angle=2\alpha\), végül \(\displaystyle F_BIA'\angle=\alpha\). Kaptuk, hogy \(\displaystyle IF_BA'\) egyenlőszárú, azaz \(\displaystyle F_BA'=F_BI=F_BC'\), így a Thalész-tétel miatt \(\displaystyle A'IC'\angle=90^{\circ}\). Hasonlóan érvelve látható, hogy ha \(\displaystyle J=F_AF_B\cap BB'\), akkor \(\displaystyle C'J\perp BH\), s így \(\displaystyle f(C'; HAB)=F_AF_B\). Analóg módon \(\displaystyle f(B'; HCA)=F_CF_B\) és \(\displaystyle f(A'; HBC)=F_BF_C\), amiből pedig \(\displaystyle F_A=A''\), \(\displaystyle F_B=B''\) és \(\displaystyle F_C=C''\) következik, ahogy állítottuk.

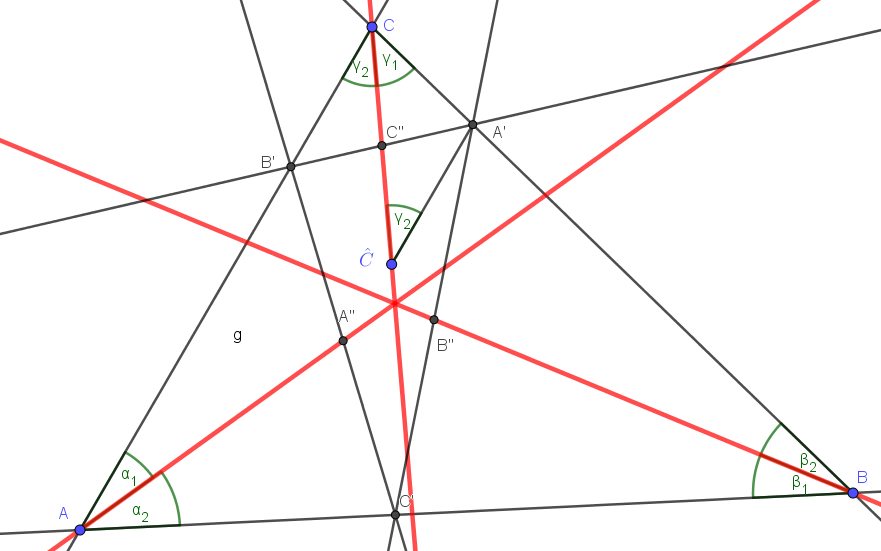
Tegyük fel, hogy az \(\displaystyle AA''\), \(\displaystyle BB''\) és \(\displaystyle CC''\) szakaszok az \(\displaystyle ABC\) szögeit rendre \(\displaystyle \alpha_1\) és \(\displaystyle \alpha_2\); \(\displaystyle \beta_1\) és \(\displaystyle \beta_2\) valamint \(\displaystyle \gamma_1\) és \(\displaystyle \gamma_2\) szögekre osztják, az ábra szerint. Legyen \(\displaystyle C\) tükörképe \(\displaystyle C''\)-re \(\displaystyle \hat C\). Mivel \(\displaystyle A'\) és \(\displaystyle B'\) szintén \(\displaystyle C''\)-re szimmetrikusan helyezkednek el, így \(\displaystyle C''\hat CA'\angle=\gamma_2\) és így \(\displaystyle C\hat CA'\triangle\)-ben a szinusz-tétel szerint \(\displaystyle \sin \gamma_1 / \sin \gamma_2=\hat CA'/A'C=CB'/CA'\). Hasonlóan belátható, hogy \(\displaystyle \sin \alpha_1 / \sin \alpha_2=AC'/AB'\) és \(\displaystyle \sin \beta_1 / \sin \beta_2=BA'/BC'\)

Mivel \(\displaystyle AA'\), \(\displaystyle BB'\) és \(\displaystyle CC'\) a magasságpontban metszi egymást, így a Ceva-tétel miatt

\(\displaystyle 1=\frac{AC'}{AB'}\cdot \frac{BA'}{BC'}\cdot \frac{CB'}{CA'}=\frac {\sin \alpha_1}{\sin \alpha_2}\cdot \frac {\sin \beta_1}{\sin \beta_2}\cdot \frac {\sin \gamma_1}{\sin \gamma_2}, \)

amiből a Ceva-tétel trigonometrikus alakja miatt következik az állítás.

Diszkusszió: Derékszögű háromszög esetén értelmezési gondokba ütközünk.

Ha \(\displaystyle ABC\) tompaszögű, és \(\displaystyle C\) a tompaszögű csúcs, akkor az érvelésben \(\displaystyle H\) és \(\displaystyle C\) szerepe felcserélődik, de a bizonyítás a hegyesszögű esethez nagyon hasonlóan történik, a részleteket az olvasóra bízzuk. A feladat állítása ebben az esetben is igaz.

1. megjegyzés A bizonyítás második része elkerülhető, ha hivatkozunk az angolul "Cevian Nest"-ként emlegetett tételre. (Legjobb tudomásunk szerint nincs a tétel nevére kialakult magyar terminológia.) A tétel lényegében azt mondja, hogy ha \(\displaystyle ABC\triangle\)-be írunk egy \(\displaystyle A'B'C'\triangle\)-t úgy, hogy \(\displaystyle AA'\), \(\displaystyle BB'\) és \(\displaystyle CC'\) konkurrensek, majd \(\displaystyle A'B'C'\triangle\)-be írunk egy \(\displaystyle A''B''C''\triangle\)-t úgy, hogy \(\displaystyle A'A''\), \(\displaystyle B'B''\) és \(\displaystyle C'C''\) konkurrensek, akkor \(\displaystyle AA''\), \(\displaystyle BB''\) és \(\displaystyle CC''\) is konkurrensek.

2. megjegyzés A feladatba sajtóhiba csúszott, a hegyesszögű jelző az \(\displaystyle ABC\) háromszögre vonatkozott szándékaink szerint, nem \(\displaystyle XYZ\)-re. Szerencsére a megoldókat az elírás nem befolyásolta. A hibáért elnézést kérünk.

Statistics:

16 students sent a solution.
6 points:	Beke Csongor, Csaplár Viktor, Győrffi Ádám György, Hegedűs Dániel, Jánosik Áron, Nagy Nándor, Osztényi József, Rareș Polenciuc, Szabó 991 Kornél, Tiderenczl Dániel, Várkonyi Zsombor, Velich Nóra, Weisz Máté.
5 points:	Kovács 129 Tamás.
4 points:	2 students.

Problems in Mathematics of KöMaL, April 2019