 |
A B. 5031. feladat (2019. május) |
B. 5031. Az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AD\) oldalának \(\displaystyle D\)-n túli meghosszabbításán vegyük fel az \(\displaystyle F\) pontot. A \(\displaystyle BF\) szakasz a \(\displaystyle CD\) oldalt a \(\displaystyle G\), az \(\displaystyle AC\) átlót pedig az \(\displaystyle E\) pontban metszi. Mutassuk meg, hogy
\(\displaystyle \frac{1}{BE}=\frac{1}{BG}+\frac{1}{BF}. \)
(3 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Megoldás.
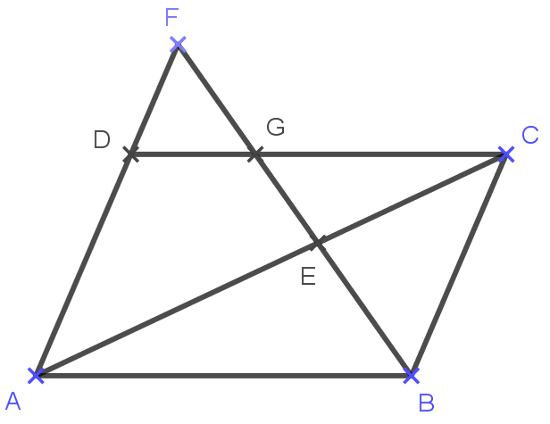
Az \(\displaystyle FB\) egyenes elválasztja a \(\displaystyle C\) pontot az \(\displaystyle A\) és \(\displaystyle D\) pontoktól, így az \(\displaystyle E\) és \(\displaystyle G\) metszéspontok biztosan az \(\displaystyle AC\), illetve a \(\displaystyle DC\) szakaszon vannak. Az \(\displaystyle ABE\) és \(\displaystyle CGE\) háromszögek hasonlók, mert \(\displaystyle E\)-nél fekvő szögeik csúcsszögek, az \(\displaystyle A\)-nál és \(\displaystyle C\)-nél, illetve \(\displaystyle B\)-nél és \(\displaystyle G\)-nél fekvő szögeik pedig váltószögek az \(\displaystyle AB\) és \(\displaystyle CD\) párhuzamossága miatt. A megfelelő oldalak aránya:
\(\displaystyle \frac{GE}{BE}=\frac{CG}{AB}.\)
Szintén hasonlók az \(\displaystyle ABF\) és \(\displaystyle CGB\) háromszögek is, mert a megfelelő szögeik váltószögek. Itt az oldalak aránya:
\(\displaystyle \frac{BG}{BF}=\frac{CG}{AB}.\)
Az arányok egyenlőségéből:
\(\displaystyle \frac{BG}{BF}=\frac{GE}{BE}=\frac{BG-BE}{BE}=\frac{BG}{BE}-1.\)
Mindkét oldalhoz \(\displaystyle 1\)-et adva és \(\displaystyle BG\)-vel osztva a bizonyítandó összefüggést kapjuk:
\(\displaystyle \frac{BG}{BF}+1=\frac{BG}{BE},\)
\(\displaystyle \frac{1}{BF}+\frac{1}{BG}=\frac{1}{BE}. \)
Statisztika:
43 dolgozat érkezett. 3 pontot kapott: Argay Zsolt, Baski Bence, Bencsik Ádám, Biczó Benedek, Bognár 171 András Károly, Bursics András, Csaplár Viktor, Fekete Richárd, Fraknói Ádám, Fülöp Csilla, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Győrffy Ágoston, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kitschner Bernadett, Kovács 129 Tamás, Laki Anna, Lovas Márton, Markó Gábor, Nagy 551 Levente, Nguyen Bich Diep, Nyitrai Boglárka, Páhán Anita Dalma, Rareș Polenciuc, Reimann Kristóf, Richlik Róbert, Sándor Péter, Sebestyén Pál Botond, Stomfai Gergely, Szabó 991 Kornél, Tálos Zoltán, Telek Zsigmond , Terjék András József, Tiderenczl Dániel, Tóth 057 Bálint, Várkonyi Zsombor, Velich Nóra. 1 pontot kapott: 3 versenyző.
A KöMaL 2019. májusi matematika feladatai

