Problem B. 5033. (May 2019)

B. 5033. The \(\displaystyle \binom{n+1}{2}\) numbers \(\displaystyle a_{1,1}, a_{1,2}, \ldots, a_{1,n}, a_{2,1}, a_{2,2}, \ldots, a_{2,n-1}, \ldots, a_{k,1}, \ldots, a_{k,n+1-k}, \ldots, a_{n,1}\) are called an inverted Pascal pyramid of order \(\displaystyle n\) if \(\displaystyle a_{k,j}=a_{k-1,j} + a_{k-1,j+1}\) for an arbitrary \(\displaystyle 2 \le k \le n\) and \(\displaystyle 1 \le j \le n+1-k\). An example of an inverted Pascal pyramid of order 3 is shown below:

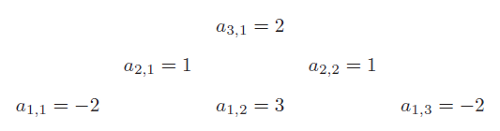
Let \(\displaystyle s_k\) denote the sum of the numbers in row \(\displaystyle k\) of the pyramid, that is, \(\displaystyle s_k = a_{k,1} + a_{k,2} + \cdots + a_{k,n+1-k}\). A pyramid is said to have a sign change in row \(\displaystyle k\) (\(\displaystyle k>1\)) if \(\displaystyle s_{k-1} \cdot s_k <0\). Given the value of \(\displaystyle n\), what is the largest possible \(\displaystyle k\) if a pyramid of order \(\displaystyle n\) has sign changes in rows 2, 3, \(\displaystyle \ldots\), \(\displaystyle k\), but no sign change in row \(\displaystyle (k+1)\)? (In the example above, \(\displaystyle k=2\) since \(\displaystyle s_1 \cdot s_2 = -2 <0\) but \(\displaystyle s_2 \cdot s_3 = 4 >0\).)

(5 pont)

Deadline expired on June 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A megoldás során \(\displaystyle n\) a piramis rendjét fogja jelölni (és a leírásban szereplő piramisok -ha máshogy nem rendelkezünk- \(\displaystyle n\)-edrendűek lesznek).
Legyen \(\displaystyle \mathcal{A}=\{ a_{1,1} ; ... ; a_{n,1} \}\) és \(\displaystyle \mathcal{B}=\{ b_{1,1} ; ... ; b_{n,1} \}\) két \(\displaystyle n\)-edrendű Pascal-piramis. Ekkor a \(\displaystyle c \mathcal{A}=\{ c \cdot a_{1,1} ; ... ; c \cdot a_{n,1} \}\), és az \(\displaystyle \mathcal{A+B}=\{ a_{1,1}+b_{1,1} ; ... ; a_{n,1} +b_{n,1}\}\) is \(\displaystyle n\)-edrendű Pascal-piramisok. (Azaz piramisok összege, piramis konstansszorosa újra piramis.)
Legyen \(\displaystyle \mathcal{E}_k\) az az "egység-piramis", ahol \(\displaystyle a_{1,1}=a_{1,2}=...=a_{1,n}=0\) és \(\displaystyle a_{1,k}=1\).
Ha a piramisom \(\displaystyle k\)-dik sorában csak az érdekel, hogy ott a sorösszeg mekkora, akkor egy piramis és a függőleges tükörtengelyére tükrözött képe (pl \(\displaystyle \mathcal{E}_k; \mathcal{E}_{n+1-k} \)) megegyezik.
Ezek alapján az \(\displaystyle \mathcal{A}\) piramis felírható az egység piramisok segítségével \(\displaystyle \mathcal{A}= a_{1,1} \cdot \mathcal{E}_1 + a_{1,2} \cdot \mathcal{E}_2 + ... + a_{1,n} \cdot \mathcal{E}_n\) alakban, és mivel csak a sorösszeget szeretnénk vizsgálni, áttérhetünk egy olyan \(\displaystyle \mathcal{A}'\) piramisra, ami bármely sorösszegét vizsgálva azonos \(\displaystyle \mathcal{A}\)-val, de az alsó sorának „második fele” (\(\displaystyle n\) páratlan volta esetén a középső mezőt kivéve) csupa nulla, jelesül \(\displaystyle \mathcal{A}'= \left( a_{1,1} + a_{1,n} \right) \cdot \mathcal{E}_1 + \left( a_{1,2} + a_{1,n-1} \right) \cdot \mathcal{E}_2 + ... + \left( a_{1,\frac{n}{2}} + a_{1,\frac{n}{2}+1} \right) \cdot \mathcal{E}_{\frac{n}{2}} + 0 \cdot \mathcal{E}_{\frac{n}{2}+1} + ... + 0 \cdot \mathcal{E}_n\) . (Ez az az eset, ha \(\displaystyle n\) páros; ha \(\displaystyle n\) páratlan, akkor \(\displaystyle \mathcal{A}'\) hasonlóan leírható.)
Ezek után esetszétválasztással megvizsgáljuk \(\displaystyle n=2k\) (páros) és \(\displaystyle n=2k+1\) (páratlan) eseteket.
I. eset: A piramisunk \(\displaystyle n=2k\) (páros) rendű.
Lemma: Azt mutatjuk meg, hogy ekkor akárhogyan is van kitöltve az alsó sor, legfeljebb \(\displaystyle k\)-ad rendben jelváltó a piramis.
Indirekt tegyük fel, hogy a piramis legalább \(\displaystyle k+1\)-ed rendben jelváltó. Legyen a piramisunk olyan, hogy alulról első sorára \(\displaystyle s_1>0\), majd második sorára \(\displaystyle s_2<0\), és így tovább... A fentiek alapján választhatunk olyan \(\displaystyle \mathcal{A}\) piramist, aminek alsó sorában az utolsó \(\displaystyle k\) darab \(\displaystyle a_{1,k+1},a_{1,k+2},...,a_{1,2k}\) elem mind 0. Ekkor persze az \(\displaystyle a_{j,l}\) számok definíciója alapján \(\displaystyle 0=a_{1,2k}=a_{2,2k-1}=a_{3,2k-2}=...=a_{k,k+1}\) (a piramis „jobb széle" egy ideig 0 elemeket tartalmaz.)
Mivel az alsó sorban lévő összes nem 0 \(\displaystyle a_{1,m}\) szám az \(\displaystyle a_{1,1} \) kivételével (\(\displaystyle 0=a_{1,n}\)!) az alulról második sorban lévő \(\displaystyle a_{2,l}\) számokban (mint összegekben) két-két helyen „szerepel”, emiatt \(\displaystyle 0>s_2 = 2 s_1 - a_{1,1} \rightarrow a_{1,1} > 2 s_1 > 0\).
Teljesen hasonlóan mivel az alulról második sorban lévő összes nem 0 \(\displaystyle a_{2,m}\) szám az \(\displaystyle a_{2,1} \) kivételével (\(\displaystyle 0=a_{2,n-1}\)!) az alulról harmadik sorban lévő \(\displaystyle a_{3,l}\) számokban (mint összegekben) két-két helyen „szerepel”, emiatt \(\displaystyle 0<s_3 = 2 s_2 - a_{2,1} \rightarrow a_{2,1} < 2 s_2 < 0\).
Ezt folytatva az alulról \(\displaystyle k\)-dik sorig (mivel \(\displaystyle 0=a_{k,k+1}\)!) adódik, hogy az \(\displaystyle a_{1,1} ; a_{3,1} ; a_{5,1} ...\) számok pozitívak, míg az \(\displaystyle a_{2,1} ; a_{4,1} ; a_{6,1} ...\) számok negatívak (és így \(\displaystyle a_{k,1}\) és \(\displaystyle a_{k+1,1}\) is ellentétes előjelű).
Most pedig a „bal oszlopban" szereplő \(\displaystyle a_{1,1};a_{2,1};...;a_{k+1,1}\) számok előjeléből fogunk következtetni az alsó sorban lévő \(\displaystyle a_{1,1};a_{1.2};...;a_{1,k}\) előjelére,és abszolútértékére!
Mivel a fenteik alapján \(\displaystyle 0<a_{1,1}\) és \(\displaystyle 0>a_{2,1} = a_{1,1} + a_{1,2}\) emiatt \(\displaystyle 0>a_{2,1} > a_{1,2}\) és \(\displaystyle |a_{1,1}|<|a_{1,2}|\).
Hasonlóan \(\displaystyle 0>a_{2,1}\) és \(\displaystyle 0<a_{3,1} = a_{2,1} + a_{2,2} = \underbrace {a_{2,1}}_{<0} + (\underbrace{a_{1,2}}_{<0} + a_{1,3})\) emiatt \(\displaystyle 0< a_{1,3}\) és \(\displaystyle |a_{1,2}|<|a_{1,3}|\). (És innen \(\displaystyle a_{2,2} = a_{1,2} + a_{1,3}\) miatt \(\displaystyle a_{2,2}>0\) is teljesül.
Tovább lépve: \(\displaystyle 0<a_{3,1}\) és \(\displaystyle 0>a_{4,1} = a_{3,1} + a_{3,2} = a_{3,1} + (a_{2,2} + a_{2,3}) = \underbrace {a_{3,1}}_{>0} + \underbrace{a_{2,2}}_{>0} + (\underbrace{a_{1,3}}_{>0}+a_{1,4}) \) emiatt \(\displaystyle 0>a_{4,1} > a_{1,4}\) és \(\displaystyle |a_{1,3}|<|a_{1,4}|\). (És \(\displaystyle 0> \underbrace {a_{3,1}}_{>0} + a_{3,2}\) miatt \(\displaystyle a_{3,2}<0\), valamint \(\displaystyle a_{2,3} = a_{1,3} + a_{1,4} < 0\) is teljesül.)
Ezt folytatva adódik, hogy az \(\displaystyle a_{1,1}; a_{1,2}; a_{1,3}; ...; a_{1,k}\) számok felváltva pozitívak, illetve negatívak, valamint \(\displaystyle |a_{1,1}| < |a_{1,2}| < |a_{1,3}| < ... < |a_{1,k}|\).
Ekkor ha \(\displaystyle k(=2m)\) páros, akkor
\(\displaystyle s_1= \underbrace {(a_{1,1} + a_{1,2})}_{<0} + \underbrace {(a_{1,3} + a_{1,4})}_{<0} + ... + \underbrace {(a_{1,2m-1} + a_{1,2m})}_{<0} + \underbrace {(a_{1,2m+1} + ...+a_{1,4m})}_{=0} <0\) ellentmondásban azzal, hogy az első sor összegére \(\displaystyle s_1>0\). míg ha \(\displaystyle k(=2m+1)\) páratlan, akkor
\(\displaystyle s_2=2s_1 - a_{1,1}= a_{1,1} + 2\underbrace {(a_{1,2} + a_{1,3})}_{>0} + 2\underbrace {(a_{1,4} + a_{1,5})}_{>0} + ... +2 \underbrace {(a_{1,2m} + a_{1,2m+1})}_{>0} + 2\underbrace {(a_{1,2m+2} + ...+a_{1,4m+2})}_{=0} >0\)
ellentmondásban azzal, hogy a második sor összegére \(\displaystyle s_2<0\).
Mivel ellentmondáshoz jutottunk, az \(\displaystyle n=2k\) (páros) magas piramis nem lehet \(\displaystyle (k+1)\)-ed rendben jelváltó.
Viszont adunk egy konstrukciót arra, hogy \(\displaystyle k\)-adrendben lehet jelváltó a piramis.
Tekintsük azt az \(\displaystyle (n+1)=(2k+1)\)-ed rendű piramist, amelynek alsó sorának számai: a „bal oldalon": \(\displaystyle a_{1,1}=1; a_{1,2}=-2 ; a_{1,3}=4;a_{1,4}=-8;...;a_{1,k}=(-2)^{k-1}\), középen:\(\displaystyle a_{1,k+1}=0\), míg a „jobb oldalon": \(\displaystyle a_{1,n+1}=-1; a_{1,n}=2 ; a_{1,n-1}=-4;...;a_{1,k+2}=a_{1,n+1-(k-1)}= -(-2)^{k-1}\). (Azaz az \(\displaystyle \mathcal{A}\) piramist a függőleges tükörtengelyére tükrözve éppen \(\displaystyle \mathcal{A}' = -\mathcal{A}\) piramist kapjuk).
Erre a piramisra \(\displaystyle s_1=s_2=...=s_n=0\) nyilván; másfelől a piramis „bal szélének" a számaira: \(\displaystyle a_{1,1}=1; a_{2,1}=-1;a_{3,1}=1;a_{4,1}=-1;...;a_{k,1}=(-1)^{k-1}\) felváltva +1/-1 értékűek az alsó \(\displaystyle k\) sorban.
Ha ennek az \(\displaystyle (n+1)\)-ed rendű \(\displaystyle \mathcal{A}\) piramisnak elhagyjuk a bal oszlopát (az \(\displaystyle a_{1,1};a_{2,1};a_{3,1};...\) elemeket), akkor egy olyan \(\displaystyle n=(2k)\)-ad rendű \(\displaystyle \mathcal{B}\) piramist kapunk, ahol a sorösszegek felváltva éppen: \(\displaystyle s(\mathcal{B})_1=s(\mathcal{A})_1-a_{1,1}=0-1=-1\); \(\displaystyle s(\mathcal{B})_2=s(\mathcal{A})_2-a_{2,1}=0-(-1)=+1\); \(\displaystyle s(\mathcal{B})_3=s(\mathcal{A})_3-a_{3,1}=0-1=-1\);... \(\displaystyle s(\mathcal{B})_k=s(\mathcal{A})_k-a_{k,1}=0-(-1)^{k-1}=(-1)^k\) azaz a piramis valóban \(\displaystyle k\)-ad rendben jelváltó. (Hasonlóan a jobb szélső elemek elhagyásával is megfelelő piramist kapnánk.)
II. eset: A piramisunk \(\displaystyle n=2k+1\) (páratlan) rendű.
Megmutatjuk, hogy ekkor a piramis maximum \(\displaystyle (k+1)\)-ed rendben jelváltó.
Ahhoz, hogy megmutassuk, hogy ilyen rendben lehet jelváltó a piramis, csak annyit kell tennünk, hogy a fenti jól megkonstruált \(\displaystyle 2k\)-rendű piramis „alá" beszúrunk be egy megfelelő sort.
Az új sor elemeit \(\displaystyle a_{0,1}, a_{0,2}, ..., a_{0,2k+1}\)-gyel fogjuk jelölni. Ha \(\displaystyle a_{0,1}\) helyett \(\displaystyle x\)-t írunk, akkor \(\displaystyle a_{0,2}=a_{1,1}-a_{0,1}=-x+a_{1,1}\), hasonlóan \(\displaystyle a_{0,3}=a_{1,2}-a_{0,2}=a_{1,2}-(a_{1,1}-x)=x+a_{1,2}-a_{1,1}\), hasonlóan \(\displaystyle a_{0,4}=a_{1,3}-a_{0,3}=a_{1,3}-(x+a_{1,2}-a_{1,1}) = -x + a_{1,3}-a_{1,2}+a_{1,1}\);...; \(\displaystyle a_{0,2k+1} = x +a_{1,2k}-a_{1,2k-1} \pm ... - a_{1,1}\).
Az alsó sor \(\displaystyle s_0\) összegére: \(\displaystyle s_0=x+(-x+a_{1,1}) + (x-a_{1,1} + a_{1,2}) + (-x+a_{1,1}-a_{1,2} + a_{1,3}) + ... + (x-a_{1,1}+a_{1,2}-a_{1,3} \pm ... + a_{1,2k}) = x + a_{1,2} + a_{1,4} + a_{1,6} + ... + a_{1,2k}\). Ekkor \(\displaystyle x\)-t megválaszthatjuk úgy is, hogy az összeg pozitív legyen és úgy is, hogy negatív, azaz elérhető, hogy \(\displaystyle s_0\) előjele más legyen, mint \(\displaystyle s_1\) előjele, de akkor a piramisunk \(\displaystyle (k+1)\)-ed rendben lesz jelváltó.
Másfelől a piramisunk nem lehet \(\displaystyle (k+2)\)-ed rendben jelváltó, mert akkor elhagyva az alsó sorát egy olyan \(\displaystyle 2k\)-ad (páros!) rendű piramist kapnánk, amely \(\displaystyle (k+1)\)-ed rendben jelváltó, ellentétben az előzőekkel.
Összefoglalva: ha a piramisunk \(\displaystyle n=2k\)-rendű, akkor legfeljebb \(\displaystyle k\)-ad rendben lehet jelváltó,
míg, ha a piramisunk \(\displaystyle n=2k+1\)-rendű, akkor legfeljebb \(\displaystyle (k+1)\)-ed rendben lehet jelváltó.

Statistics:

13 students sent a solution.
5 points:	Weisz Máté.
4 points:	Beke Csongor.
3 points:	3 students.
2 points:	2 students.
1 point:	5 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, May 2019