Problem B. 5038. (September 2019)

B. 5038. Let \(\displaystyle P\) be a point in the interior of a regular octagon \(\displaystyle ABCDEFGH\). Show that the sum of the areas of triangles \(\displaystyle ABP\), \(\displaystyle CDP\), \(\displaystyle EFP\) and \(\displaystyle GHP\) equals the sum of the areas of triangles \(\displaystyle BCP\), \(\displaystyle DEP\), \(\displaystyle FGP\) and \(\displaystyle HAP\).

(3 pont)

Deadline expired on October 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha \(\displaystyle XY\) és \(\displaystyle ZT\) a szabályos nyolcszög két, egymással szemköztes oldala, akkor e két oldalszakasz egymással párhuzamos és egyenlő. Ezért a \(\displaystyle PXY\) és \(\displaystyle PZT\) háromszögek \(\displaystyle P\)-ből induló magasságvonalai egy egyenesbe esnek, és a magasságok összege egyenlő az \(\displaystyle XY\) és \(\displaystyle ZT\) oldalak \(\displaystyle m\) távolságával. Így – a nyolcszög oldalának hosszát \(\displaystyle a\)-val jelölve – a két háromszög területének összege:

\(\displaystyle t_{PXY}+t_{PZT}=\frac{am_1}{2}+\frac{am_2}{2}=\frac{am}{2}.\)

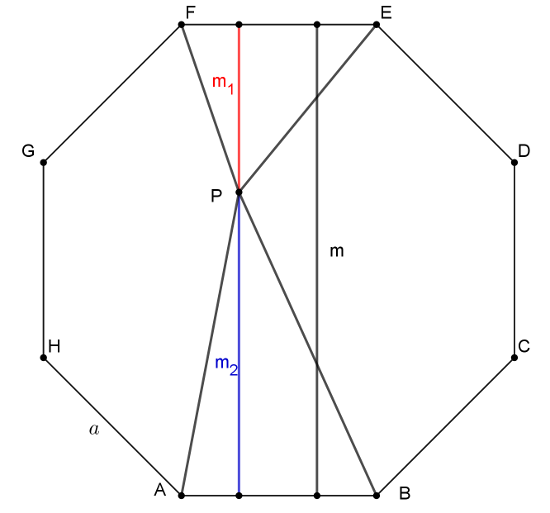
Tehát

\(\displaystyle t_{PAB}+t_{PEF}=t_{PBC}+t_{PFG}=t_{PCD}+t_{PGH}=t_{PDE}+t_{PHA}(=\frac{am}{2}), \)

amiből következik, hogy a \(\displaystyle ABP\), \(\displaystyle CDP\), \(\displaystyle EFP\) és \(\displaystyle GHP\) háromszögek területének összege, illetve a \(\displaystyle BCP\), \(\displaystyle DEP\), \(\displaystyle FGP\) és \(\displaystyle HAP\) háromszögek területének összege egyaránt \(\displaystyle {am}\).

Statistics:

203 students sent a solution.
3 points:	181 students.
2 points:	13 students.
1 point:	7 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, September 2019