Problem B. 5040. (September 2019)

B. 5040. In a square \(\displaystyle ABCD\), let \(\displaystyle F\) be an interior point of side \(\displaystyle AB\), and let \(\displaystyle E\) be an interior point of side \(\displaystyle AD\). Draw a perpendicular to line \(\displaystyle CE\) at point \(\displaystyle E\), and a perpendicular to line \(\displaystyle CF\) at point \(\displaystyle F\). Denote the intersection of the two perpendiculars by \(\displaystyle M\). Given that the area of triangle \(\displaystyle CEF\) is half the area of pentagon \(\displaystyle BCDEF\), prove that point \(\displaystyle M\) lies on diagonal \(\displaystyle AC\) of the square.

(4 pont)

Deadline expired on October 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha a \(\displaystyle CEF\) háromszög területe fele a \(\displaystyle BCDEF\) ötszögének, akkor \(\displaystyle T_{CEF} = T_{CDE} + T_{CFB}\).

Forgassuk el a négyzetünket a \(\displaystyle C\) pont körül \(\displaystyle 90^{\circ}\)-kal úgy, hogy a \(\displaystyle D\) pont képe a \(\displaystyle B\)-be kerüljön.

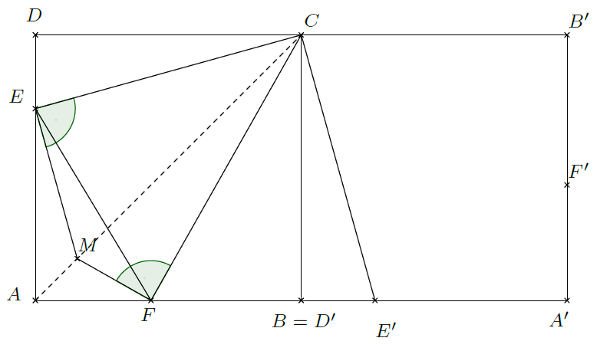
Mivel \(\displaystyle T_{CDE} = T_{CD'E'}\), ezért \(\displaystyle T_{CEF} = T_{CE'F}\). Másfelől a \(\displaystyle CEF\) háromszögnek és a \(\displaystyle CE'F\) háromszögnek a \(\displaystyle CF\) oldala közös, míg \(\displaystyle CE=CE'\). Emiatt a területük csak úgy lehet egyenlő, ha a két megfelelő oldal által közbezárt szög is egyenlő. Tehát a két háromszög egybevágó.

\(\displaystyle CEF \cong CE'F\) miatt \(\displaystyle CFE \sphericalangle = CFE' \sphericalangle\) és így \(\displaystyle CED \sphericalangle = CE'D' \sphericalangle = CEF \sphericalangle\), azaz a \(\displaystyle CE\) és a \(\displaystyle CF\) szakaszok felezik a \(\displaystyle DEF \sphericalangle\), illetve az \(\displaystyle EFB \sphericalangle\) szögeket, vagyis \(\displaystyle CE\) és \(\displaystyle CF\) az \(\displaystyle AFE\) háromszög megfelelő külső szögfelezői. Emiatt \(\displaystyle EM\) és \(\displaystyle FM\) belső szögfelezők az \(\displaystyle AFE\) háromszögben. Tehát \(\displaystyle M\) az \(\displaystyle AFE\)-be beírható kör középpontja, de akkor a harmadik belső szögfelező is átmegy rajta, és ez (mivel \(\displaystyle AEF \sphericalangle = 90^{\circ}\)) éppen az \(\displaystyle AC\) átló. Ezzel az állítást igazoltuk.

(Diszkusszió: Az \(\displaystyle E\), \(\displaystyle F\) pontok választása miatt (a terület feltétel miatt nincs elfajuló eset) nyilván előáll \(\displaystyle M\).)

Statistics:

64 students sent a solution.
4 points:	52 students.
3 points:	2 students.
2 points:	2 students.
1 point:	5 students.
0 point:	1 student.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, September 2019