 Problem B. 5041. (September 2019)
Problem B. 5041. (September 2019)
B. 5041. An \(\displaystyle n \times n\) table of real numbers in each field is called a zero square if the sum of the numbers in every \(\displaystyle 2 \times 2\) square part of it (therefore in the whole table, too) is zero. (The diagram shows a \(\displaystyle 3\times3\) example.)
| 2 | -3 | 4 |
| -4 | 5 | -6 |
| 1 | -2 | 3 |
What is the largest possible \(\displaystyle n\) for which there exists an \(\displaystyle n \times n\) zero square such that the entries are not all zeros?
(5 pont)
Deadline expired on October 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először megmutatjuk, hogy \(\displaystyle n=7\) esetén már nincs nemtriviális nullnégyzet, majd \(\displaystyle n=6\) esetén adunk egy nemtriviális kitöltést.
Tekintsünk először egy \(\displaystyle 4 \times 4\)-es nullnégyzetet, és a mezőiben szereplő számokat jelöljük rendre \(\displaystyle a_{1,1}, a_{1,2}, a_{1,3}, a_{1,4}, a_{2,1}, ..., a_{4,4}\)-gyel.
| \(\displaystyle a_{1,1}\) | \(\displaystyle a_{1,2}\) | \(\displaystyle a_{1,3}\) | \(\displaystyle a_{1,4}\) |
| \(\displaystyle a_{2,1}\) | \(\displaystyle a_{2,2}\) | \(\displaystyle a_{2,3}\) | \(\displaystyle a_{2,4}\) |
| \(\displaystyle a_{3,1}\) | \(\displaystyle a_{3,2}\) | \(\displaystyle a_{3,3}\) | \(\displaystyle a_{3,4}\) |
| \(\displaystyle a_{4,1}\) | \(\displaystyle a_{4,2}\) | \(\displaystyle a_{4,3}\) | \(\displaystyle a_{4,4}\) |
Bevezetjük a következő jelölést: az \(\displaystyle a_{i,j}\) és az \(\displaystyle a_{i+k,j+k}\) sarokmezők által meghatározott nullnégyzetet az \(\displaystyle \left(\left( a_{i,j};a_{i+k,j+k} \right) \right)\) módon fogjuk jelölni.
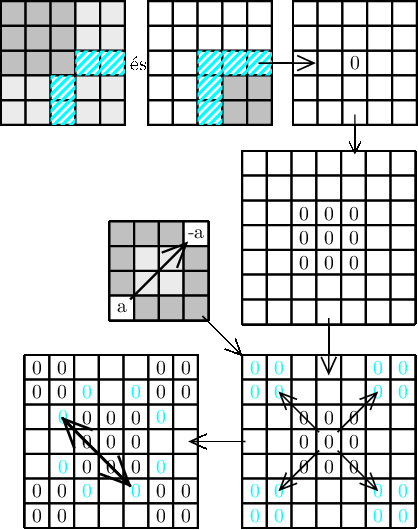
Az \(\displaystyle \left(\left( a_{1,1};a_{3,3} \right) \right)\) \(\displaystyle 3 \times 3\)-as nullnégyzetnek az \(\displaystyle a_{2,2}, a_{2,3}, a_{3,2}, a_{3,3}\) mezők által meghatározott \(\displaystyle 2 \times 2\)-es nullnégyzet a része, emiatt a kimaradó 5 elem összege 0, azaz \(\displaystyle a_{1,1}+a_{1,2}+a_{1,3}+a_{2,1}+a_{3,1} = 0\).
Hasonlóan az \(\displaystyle \left(\left( a_{2,2};a_{4,4} \right) \right)\) \(\displaystyle 3 \times 3\)-as nullnégyzetnek is része az \(\displaystyle a_{2,2}, a_{2,3}, a_{3,2}, a_{3,3}\) mezők által meghatározott \(\displaystyle 2 \times 2\)-es nullnégyzet, azaz \(\displaystyle a_{4,2}+a_{4,3}+a_{4,4}+a_{2,4}+a_{3,4} = 0\).
Másfelől mivel a kiinduló \(\displaystyle 4 \times 4\)-es nullnégyzetünkben is 0 az elemek összege és az ebben a négyzetben szereplő számok pontosan a középső \(\displaystyle 2\times2\)-es nullnégyzet, a két "oldalt kimaradó" 5-5 nulla összegű elem, illetve \(\displaystyle a_{1,4}\) és \(\displaystyle a_{4,1}\), ezért \(\displaystyle a_{4,1} + a_{1,4} = 0\). Innen nyilvánvalóan következik, hogy egy legalább négy méretű nullnégyzetben az egymástól átlósan három távolságra lévő mezőpárok esetén ezen mezők számainak összege 0; azaz \(\displaystyle a_{i,j}+a_{i+3,j+3}=0\), illetve \(\displaystyle a_{i,j}+a_{i+3,j-3}=0\).
Nagyobb \(\displaystyle (k+1) \times (k+1)\)-es (\(\displaystyle k>3\)) nullnégyzetből kiindulva pontosan ugyanígy megmutatható, hogy az egymástól átlósan \(\displaystyle k\) távolságra lévő mezőpárok esetén ezen mezők számainak összege is 0; azaz \(\displaystyle a_{i,j}+a_{i+k,j+k}=0\), illetve \(\displaystyle a_{i,j}+a_{i+k,j-k}=0\).
Ezek után vizsgáljunk egy \(\displaystyle 5 \times 5\) méretű nullnégyzetet (a mezőket \(\displaystyle a_{1,1}\)-től \(\displaystyle a_{5,5}\)-ig jelöljük).
Az \(\displaystyle \left(\left( a_{3,3};a_{5,5} \right) \right)\), valamint az \(\displaystyle \left(\left( a_{4,4};a_{5,5} \right) \right)\) nullnégyzet volta miatt (az előzőekhez hasonlóan) a kimaradó 5 elem összegére: \(\displaystyle a_{3,3}+a_{3,4}+a_{3,5}+a_{4,3}+a_{5,3}=0\).
Másfelől a teljes \(\displaystyle 5 \times 5\)-ös nullnégyzetünk előáll az \(\displaystyle \left(\left( a_{1,1};a_{3,3} \right) \right)\), az \(\displaystyle \left(\left( a_{1,4};a_{2,5} \right) \right)\), a \(\displaystyle \left(\left( a_{4,1};a_{5,2} \right) \right)\) és a \(\displaystyle \left(\left( a_{4,4};a_{5,5} \right) \right)\) nullnégyzetek, valamint a négy kimaradó \(\displaystyle a_{3,4}, a_{3,5}, a_{4,3}, a_{5,3}\) mezők diszkrét uniójaként. Emiatt \(\displaystyle a_{3,4}+a_{3,5}+a_{4,3}+a_{5,3}=0\) és így \(\displaystyle a_{3,3}=0\), azaz egy \(\displaystyle 5 \times 5\)-ös nullnégyzet középső mezőjén csak 0 állhat.
Most már térjünk rá a \(\displaystyle 7 \times 7\)-es eset tárgyalására!
A \(\displaystyle 7\times 7\)-es nullnégyzet középső \(\displaystyle \left(\left( a_{3,3};a_{5,5} \right) \right)\) 9 mezője közül valamennyi egy megfelelő \(\displaystyle 5 \times 5\) méretű nullnégyzet középső mezője, azaz mindegyik helyen 0 áll.
Ezért a tőlük átlósan 3-ra lévő mezőkön is csak 0 állhat az \(\displaystyle a_{i,j}+a_{i+3,j+3}=0\), illetve \(\displaystyle a_{i,j}+a_{i+3,j-3}=0\) szabályok miatt; azaz a nagy nullnégyzet \(\displaystyle \left(\left( a_{1,1};a_{2,2} \right) \right)\)-es, \(\displaystyle \left(\left( a_{6,1};a_{7,2} \right) \right)\) -es, \(\displaystyle \left(\left( a_{1,6};a_{2,7} \right) \right)\)-es és \(\displaystyle \left(\left( a_{6,6};a_{7,7} \right) \right)\)-es részeiben szintén minden szám 0.
Innen \(\displaystyle a_{2,3}=a_{3,2}=a_{5,2}=a_{6,3}=a_{3,6}=a_{5,2}=a_{5,6}=a_{6,5}=0\), mert minden ilyen mező átlósan négy távolságra van az imént vizsgált \(\displaystyle 2\times2\) méretű csupa 0 számot tartalmazó nullnégyzet egy-egy mezőjétől. (Például az \(\displaystyle a_{1,2}=0\) mezőtől négy távol van az \(\displaystyle a_{1+4,2+4} = a_{5,6}\) mező).
A még nem tárgyalt mezők esetén pedig rendre mindegyik mezőhöz van olyan \(\displaystyle 2 \times 2\)-es méretű nullnégyzet, amelynek három már ismert eleme mind 0, azaz a kimaradó mezők is mind 0-k.
Vagyis nincs nemtriviális \(\displaystyle 7\times7\) méretű nullnégyzet.
A leírt bizonyítás lépéseit szemlélteti az alábbi ábra:
\(\displaystyle n=6\) esetre pedig adható példa:
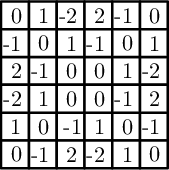
Azaz legfelejebb \(\displaystyle 6 \times6\)-os méretben létezik nemtriviális nullnégyzet.
Statistics:
85 students sent a solution. 5 points: 58 students. 4 points: 1 student. 3 points: 1 student. 2 points: 5 students. 1 point: 5 students. 0 point: 13 students. Not shown because of missing birth date or parental permission: 2 solutions.
Problems in Mathematics of KöMaL, September 2019
