Problem B. 5047. (October 2019)

B. 5047. In a right-angled triangle \(\displaystyle ABC\), point \(\displaystyle D\) lies in the interior of leg \(\displaystyle AC\), and point \(\displaystyle E\) lies on the extension of hypotenuse \(\displaystyle AB\) beyond \(\displaystyle B\). The second intersection of circles \(\displaystyle ADE\) and \(\displaystyle BCE\) (different from \(\displaystyle E\)) is \(\displaystyle F\). Show that \(\displaystyle \angle CFD=90^\circ\).

(4 pont)

Deadline expired on November 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Először gondoljuk meg, hogy az \(\displaystyle F\) pont tényleg létezik, és csak az \(\displaystyle ABC\) háromszög belsejében lehet.

Jelöljük az \(\displaystyle ADE\) kört \(\displaystyle k_1\)-gyel, a \(\displaystyle BCE\) kört \(\displaystyle k_2\)-vel. Az \(\displaystyle B\) pont belső, a \(\displaystyle C\) pedig külső pontja \(\displaystyle k_1\)-nek, mert \(\displaystyle B\) a kör \(\displaystyle AE\) húrjának belsejében, \(\displaystyle C\) pedig az \(\displaystyle AD\) húr meghosszabításán fekszik. A \(\displaystyle k_2\) kör mindkét \(\displaystyle BC\) íve a \(\displaystyle k_1\)-nek egy belső és egy külső pontját köti össze, ezért mindkét \(\displaystyle BC\) ív elmetszi \(\displaystyle k_1\)-t; a két metszéspont \(\displaystyle E\) és \(\displaystyle F\). Ezek a \(\displaystyle BC\) egyenes két oldalán vannak; \(\displaystyle E\) az \(\displaystyle A\)-val ellentétes, \(\displaystyle F\) az \(\displaystyle A\)-val megegyező oldalon. A \(\displaystyle BECF\) egy konvex négyszög.

Mivel \(\displaystyle FCB\measuredangle = FEB\measuredangle < CEB\measuredangle < CBA\measuredangle < ACB\measuredangle\), a \(\displaystyle CF\) félegyenes az \(\displaystyle ACB\) szögtartományba esik. Hasonlóan, \(\displaystyle CBF\measuredangle = CEF\measuredangle < CEB\measuredangle < CBA\measuredangle\) miatt a \(\displaystyle BF\) félegyenes a \(\displaystyle CBA\) szögtartományban fekszik. A kettő metszéspontja, \(\displaystyle F\) az \(\displaystyle ABC\) háromsög belsejében van, így az \(\displaystyle ADFE\) húrnégyszög is konvex.

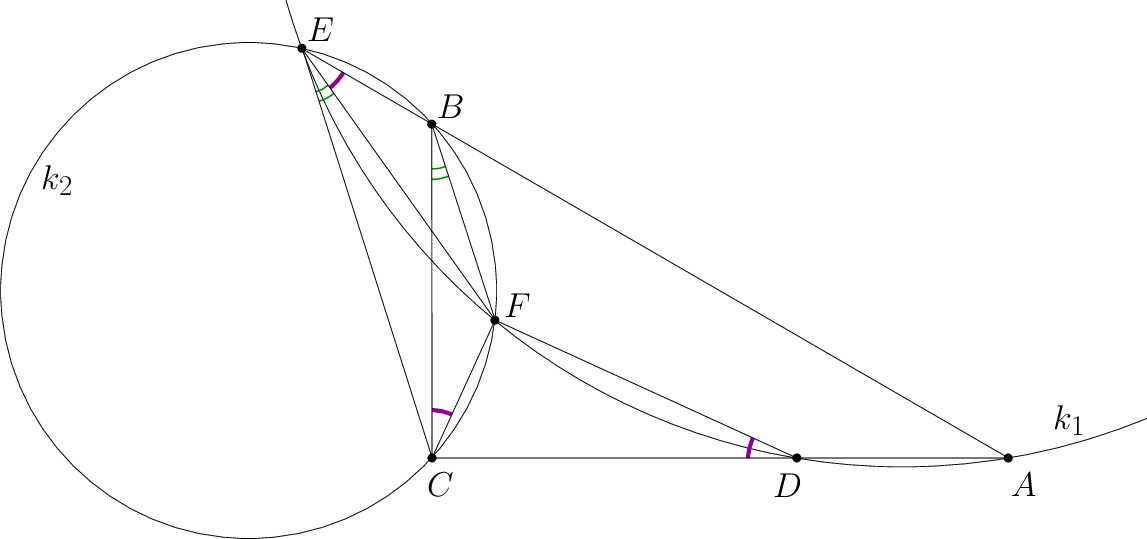
A két húrnégyszögben

\(\displaystyle FDC\measuredangle = 180^\circ-ADF\measuredangle = FEA\measuredangle = FEB\measuredangle = FCB\measuredangle = 90^\circ-DCF\measuredangle. \)

A \(\displaystyle CDF\) háromszög \(\displaystyle C\)-nél és \(\displaystyle D\)-nél fekvő szögeinek összege derékszög, tehát \(\displaystyle CFD\measuredangle\) is derékszög.

Megjegyzések. 1. A diszkusszió elkerülhető, ha irányított (modulo \(\displaystyle 180^\circ\)) szögekkel számolunk.

2. A feladatban szereplő elrendezés a Miquel-tétel egy határesete: ha \(\displaystyle ABC\) tetszőleges háromszög, \(\displaystyle G\), \(\displaystyle D\), \(\displaystyle E\) rendre a \(\displaystyle BC\), \(\displaystyle AC\), illetve az \(\displaystyle AB\) egyenesek egy-egy pontja, akkor az \(\displaystyle ADE\), \(\displaystyle BEG\) és \(\displaystyle CDG\) körök egy ponton mennek át. Esetünkben \(\displaystyle G\) egybeesik a \(\displaystyle C\) ponttal, ezért a \(\displaystyle CDG\) kör az a kör, amely átmegy \(\displaystyle C\)-n és \(\displaystyle D\)-n, és érinti a \(\displaystyle BC\) oldalt. A három kör közös pontja \(\displaystyle F\).

Statistics:

83 students sent a solution.
4 points:	78 students.
2 points:	1 student.
1 point:	2 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, October 2019